要旨:Sarvas 式から導かれる脳磁図解析の原則を明示する。
前項では、Sarvas 式を確認した。すなわち、
仮想球中心を位置の原点 \(\boldsymbol{O}\) とする。電流モーメント \(\boldsymbol{q}\) の電流双極子 equivalent curret dipole (ECD) が位置 \(\boldsymbol{r_0}\) にあるとき、位置 \(\boldsymbol{r}\) における磁場 \(\boldsymbol{b}\) を考える。
ただし、真空の透磁率を \(\mu_0\) とし、すべての位置において透磁率は \(\mu_0\) に等しいものとする。
Sarvas式はこの条件の下で以下の解析解を与える。
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi F^2}(F\boldsymbol{q}\times\boldsymbol{r_0}-\boldsymbol{q}\times\boldsymbol{r_0}\cdot\boldsymbol{r}\boldsymbol{\nabla}F) $$
ただし、
$$ \boldsymbol{\nabla}F=(r^{-1}a^2+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r}+2a+2r)\boldsymbol{r}-(a+2r+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r})\boldsymbol{r_0} $$
$$ F=a(ra+r^2-\boldsymbol{r_0}\cdot\boldsymbol{r}),\hspace{10pt}\boldsymbol{a}=\boldsymbol{r}-\boldsymbol{r_0},\hspace{10pt}a=|\boldsymbol{a}|,\hspace{10pt}r=|\boldsymbol{r}| $$
この Sarvas 式が示す以下の原則は重要だ
- 脳磁図解析においては、仮想球中心の座標 \(\boldsymbol{O}\) を必要とする
- 脳磁図解析において逆問題を解くことは、電流双極子の電流モーメント \(\boldsymbol{q}\) と位置 \(\boldsymbol{r_0}\) を議論することに他ならない
- 仮想球中心 \(\boldsymbol{O}\) にある電流双極子は磁場を発生しない
- 電流モーメント \(\boldsymbol{q}\) のうち、仮想球中心 \(\boldsymbol{O}\) に対して垂直な成分は磁場を発生しない(脳磁図においては議論ができない)
- 磁場 \(\boldsymbol{b}(\boldsymbol{r})\) は電流双極子の電流モーメント \(\boldsymbol{q}\) に対して線形である
- 磁場 \(\boldsymbol{b}(\boldsymbol{r})\) は電流双極子の位置 \(\boldsymbol{r_0}\) に対して非線形である
原則 1. は Sarvas 式が球対称な導体を仮定していることから自明だ。
原則 2. も Sarvas 式が電流双極子を仮定していることから自明だ。
原則 3. & 4.は Sarvas 式の第1項、第2項に\(\boldsymbol{q}\times\boldsymbol{r_0}\) が共通して出てくることから自明だ。外積の大きさは下図のように 2 つのベクトルの絶対値と正弦角の積(2つのベクトルがつくる平行四辺形の面積)だから、電流双極子が原点にある( \(\boldsymbol{r_0}\) がゼロベクトル)か、電流双極子の電流モーメント \(\boldsymbol{q}\) と位置 \(\boldsymbol{r_0}\) が平行であればその外積の大きさはゼロとなる。
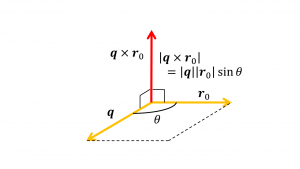
これは垂直な成分が存在しない訳ではなく、脳磁図で議論ができないというだけなので注意が必要だ。垂直な成分を議論するなら脳波を検討するのが一般的だ。
原則 5. は Sarvas 式の元となる Biot-Savart式より、電流と磁場には重ね合わせの原理が働くから、磁場は複数の電流源から発生した磁場の和として構成される(加法性を持つ)。また、Sarvas 式の第1項、第2項から電流モーメント \(\boldsymbol{q}\) の大きさに磁場 \(\boldsymbol{b}\) が比例する(斉次性を持つ)。
電流双極子の位置が決まっていれば電流モーメントとそこから発生する磁場の関係は線形であるので、\(\boldsymbol{b}=\boldsymbol{L}\boldsymbol{q}\) といったように行列で記述ができる。これは、位置が決まっていれば逆問題を解くことが容易だということだ。なお、行列 \(\boldsymbol{L}\) を磁場計算行列 Lead Field Matrix (LFM)という。
加えて、電流双極子の推定は single dipole にみならず、multi dipole も許容していることも同時に示している(優決定解である Multi ECD, 劣決定解である空間フィルターなど)。
原則 6. の線形でないことは \(\boldsymbol{\nabla}F\) や \(F\) の複雑さから自明だ。
この性質は逆問題を解く際に重要だ。電流源の推定においては電流モーメント \(\boldsymbol{q}\) と位置 \(\boldsymbol{r_0}\) の双方が不明であり、位置の非線形性から空間の探索を要する。
まとめ:Sarvas 式により脳磁図解析の原則を確認することができた。
次項では、磁場計算行列 Lead Field Matrix (LFM) の概念を導入する準備として、Sarvas 式により実際のセンサー群(センサーアレイ)にどのように信号が生じるかを検討して、磁場 \(\boldsymbol{b}(\boldsymbol{r})\) をセンサーアレイの出力に対応させたい。
(引用)
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.