要旨：ECD 推定は議論する格子点が１つであり、センサー数より圧倒的に少ないので、逆問題の解は優決定解として定型的かつ解析的に求まる。
順問題の解であるSarvas式より、電流双極子の位置が定まれば電流モーメント \( \boldsymbol{q} \) と磁場 \( \boldsymbol{b} \) の間には線形な対応関係（線形写像）が成立し、その対応（写像）を Lead Field Matrix (LFM) と呼ぶのであった。
すなわち、LFM を \( \boldsymbol{L} \) とすると、
$$ \boldsymbol{b}=\boldsymbol{L}\boldsymbol{q} $$
と行列演算の形で表現できる。
ここから逆に、磁場から電流モーメントを推定する
$$ \boldsymbol{q}=\boldsymbol{L}^-\boldsymbol{b} $$
の線形な逆の対応関係（逆線形写像） \(\boldsymbol{L}^{-}\) を求めたい。これを逆問題 Inverse Problem という（下図）。
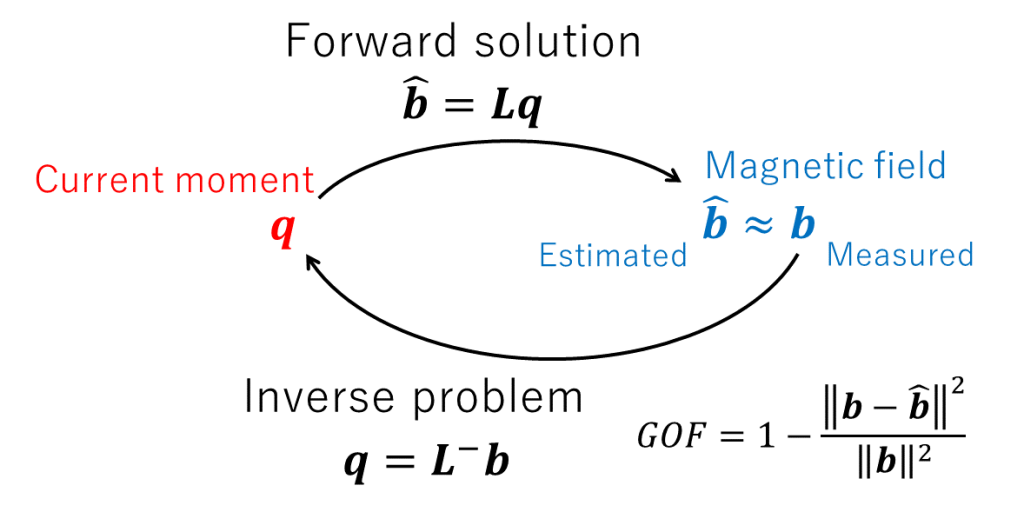
順問題での議論から、センサーアレイの数を M、格子点 N 個のうち LFM を構成する数を \(N_{LFM}\) とすると、 \(\boldsymbol{b}\) は M 次元の列ベクトル、 \(\boldsymbol{q}\) は \(2N_{LFM}\) 次元の列ベクトル、\( \boldsymbol{L} \) は \( M\times2N_{LFM} \) の行列となるのであった。
\(M>2N_{LFM}\) の状況を優決定系 overdetermined system といい、いわば情報過多の状態だ。Single-dipole 推定は M=204 or 306 に対して \(N_{LFM}=1\) であり、典型的な優決定系の解だ。
以下では n 番目の格子点について電流モーメント \( \boldsymbol{q} \) を推定することを考える。\(N_{LFM}=1\) であり、
$$ \boldsymbol{L}=\boldsymbol{L}_{n}=\left(\begin{array}{cccc}\boldsymbol{l}_{n}^\theta &\boldsymbol{l}_{n}^\phi \\\end{array}\right) $$
$$ \boldsymbol{q}=\boldsymbol{q}_{n}=\left(\begin{array}{cccc}q_{n}^\theta &q_{n}^\phi \\\end{array}\right)^T $$
だ。測定磁場 \( \boldsymbol{b} \) から電流モーメント \( \boldsymbol{q} \) を推定できれば、以下のような図が得られることが期待できる。
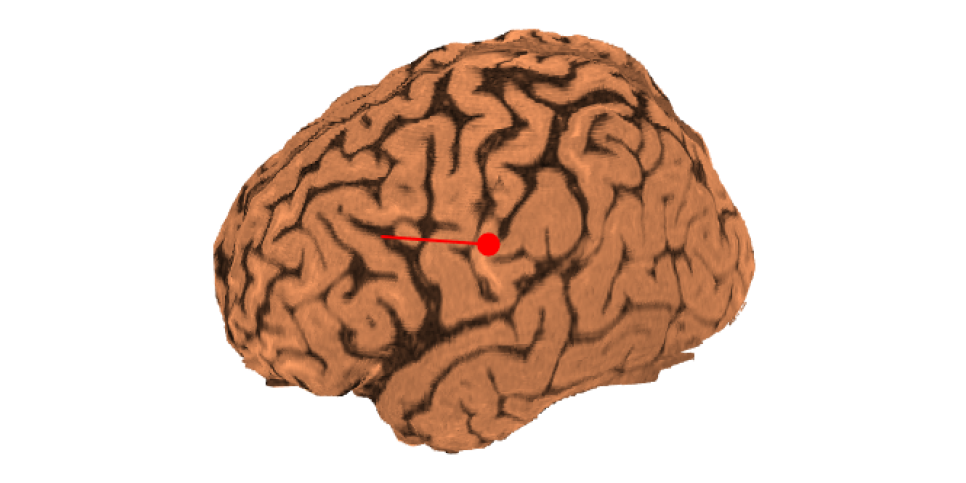
このとき、測定磁場 \( \boldsymbol{b} \) に、推定磁場 \( \boldsymbol{\hat{b}} \) ができるだけ近くなるよう、電流モーメント \( \boldsymbol{q} \) を推定したい。これは数学的には最小二乗解という定型的な優決定解 overdetermined solution だ。
すなわち、\(\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|\) が最小になる \( \boldsymbol{q} \) を求める。この際に、計算の都合上から二乗の形 \(\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2\) にするのが常套手段だ。
$$ \boldsymbol{q}=\underset{\boldsymbol{q}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2=\underset{\boldsymbol{q}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q}\|^2 $$
と定まる。
測定値と推定値の近さを表す指標を \(J=\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2=\|\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q}\|^2\) とおくと、
$$ J=(\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q})^T(\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q})=\boldsymbol{b}^T\boldsymbol{b}-\boldsymbol{b}^T\boldsymbol{Lq}-\boldsymbol{q}^T\boldsymbol{L}^T\boldsymbol{b}+\boldsymbol{q}^T\boldsymbol{L}^T\boldsymbol{L}\boldsymbol{q} $$
これが最小値を取るとき、
$$ \frac{\partial J}{\partial \boldsymbol{q}}=-2\boldsymbol{L}^T\boldsymbol{b}+2(\boldsymbol{L}^T\boldsymbol{L})\boldsymbol{q}=0 $$
すなわち、
$$ \boldsymbol{q}=\boldsymbol{L}^{-}\boldsymbol{b}=(\boldsymbol{L}^T\boldsymbol{L})^{-1}\boldsymbol{L}^T\boldsymbol{b} $$
であり、
$$ \boldsymbol{L}^{-}=(\boldsymbol{L}^T\boldsymbol{L})^{-1}\boldsymbol{L}^T $$
と求まる。
なお、測定磁場 \(\boldsymbol{b}\) と推定磁場 \(\boldsymbol{\hat{b}}\) を比較した基準 \(J=\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2\) を用いて、推定のあてはまりの良さGoodness of fit (GOF)を考えることができる [1]。
$$ GOF=1-\frac{\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2}{\|\boldsymbol{b}\|^2} $$
実際の推定では、GOF が最大化する位置を、信号が存在しうる空間（脳全体または脳のうち興味のある領域）に関して探索することになる。任意の位置 \(\boldsymbol{r}\) について
$$ \boldsymbol{q}_{\boldsymbol{r}}=\underset{\boldsymbol{q}_{\boldsymbol{r}}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{L}_{\boldsymbol{r}}\boldsymbol{q}_{\boldsymbol{r}}\|^2=(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b} $$
だから、
$$ \boldsymbol{r}=\underset{\boldsymbol{r}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{L}_{\boldsymbol{r}}(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b}\|^2 $$
となって \(\boldsymbol{r}\) が定まり、同時に \(\boldsymbol{q}\) も定まる
$$ \boldsymbol{q}=(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b} $$
これは Equivalent Current Dipole (ECD) 推定とか Single-dipole estimation などと呼ばれ、脳磁図解析におけるゴールドスタンダードだ [2]。これについては次節で考察していくことにしたい。
まとめ：測定磁場 \(\boldsymbol{b}\) に対する電流モーメント \(\boldsymbol{q}=\boldsymbol{q}_{n}\) の解は優決定解であり、LFM \(\boldsymbol{L}=\boldsymbol{L}_{n}\) を用いると \(\boldsymbol{q}=\boldsymbol{L}^{-}\boldsymbol{b}=(\boldsymbol{L}^T\boldsymbol{L})^{-1}\boldsymbol{L}^T\boldsymbol{b}\) と記述できる。
次項では、空間フィルターのように議論する電流双極子の数が格子点の数（全脳5mmボクセルならN>10,000）と同じで、センサー数M(=204 or 306)より圧倒的多い状況（劣決定系）での逆問題の解を求めることを考えたい。
（引用）
- E Kaukoranta, M Hämäläinen, J Sarvas, R Hari: Mixed and sensory nerve stimulations activate different cytoarchitectonic areas in the human primary somatosensory cortex SI. Neuromagnetic recordings and statistical considerations. Exp Brain Res. 1986;63(1):60-6.
- Iida K, Otsubo H, Matsumoto Y, Ochi A, Oishi M, Holowka S, Pang E, Elliott I, Weiss SK, Chuang SH, Snead OC 3rd, Rutka JT. Characterizing magnetic spike sources by using magnetoencephalography-guided neuronavigation in epilepsy surgery in pediatric patients. J Neurosurg. 2005 Mar;102(2 Suppl):187-96.