要旨:空間フィルターで議論する格子点の数は、信号が存在しうる全ての空間(典型的には全脳)におよび、センサー数より圧倒的に多いので、逆問題の解は劣決定解として定型的かつ解析的に求まる。
前項では、脳の一部に脳活動を支配する強い活動が想定されるような、電流双極子の数がごく少数の時に適応できる優決定系の解を求めた。
今度は、脳全体が活動していると想定されるような、電流双極子の数が多数ある場合に適応できる劣決定系の解を求めたい。
電流双極子の位置が定まった状態で、電流モーメント \(\boldsymbol{q}\) と磁場 \(\boldsymbol{b}\) の間に成立する線形写像は、LFM を \( \boldsymbol{L} \) とすると、
$$ \boldsymbol{b}=\boldsymbol{L}\boldsymbol{q} $$
磁場から電流モーメントを推定する
$$ \boldsymbol{q}=\boldsymbol{L}^-\boldsymbol{b} $$
の逆の対応関係(逆線形写像) \(\boldsymbol{L}^{-}\) を求めたい。
センサーアレイの数を M、格子点 N 個のうち LFM を構成する数を \(N_{LFM}\) とすると、 \(\boldsymbol{b}\) は M 次元の列ベクトル、 \(\boldsymbol{q}\) は \(2N_{LFM}\) 次元の列ベクトル、\( \boldsymbol{L} \) は \( M\times2L_{LFM} \) の行列となる。
ここまでは前項と同様だ。
空間フィルターでは基本的に、脳全体の多数の格子点にそれぞれ電流双極子があって磁場が発生していると仮定しており、\(M<2N_{LFM}\) の状況だ(M=204 or 306に対して、全脳5mmボクセルならN>10,000)。この状況は劣決定系underdetermined systemといい、いわば情報不足の状態だ。
この仮定は、単一の電流双極子を仮定する Single-dipole estimation よりも脳の活動としては生理的に近いと考えることもできるが、劣決定系ゆえに空間分解が低いことが欠点だ。とはいえ、その柔軟性から研究においてよく使用される手法だ。
以下では N 個の全格子点について電流モーメント \( \boldsymbol{q} \) を推定することを考える。 \(N_{LFM}=N\) であり、
$$ \boldsymbol{L}=\boldsymbol{L}_{all}=\left(\begin{array}{cccc}\boldsymbol{l}_{1}^\theta&\boldsymbol{l}_{1}^\phi & \ldots & \ldots & \boldsymbol{l}_{N}^\theta &\boldsymbol{l}_{N}^\phi \\\end{array}\right) $$
$$ \boldsymbol{q}=\boldsymbol{q}_{all}=\left(\begin{array}{cccc}q_{1}^\theta & q_{1}^\phi & \ldots & \ldots & q_{N}^\theta & q_{N}^\phi \\\end{array}\right)^T $$
だ。測定磁場 \( \boldsymbol{b} \) から全格子点の電流モーメント \(\boldsymbol{q}=\boldsymbol{q}_{all} \) を推定できれば、電流の強さ上位1%の格子点を、強いものほど大きく白く表示すると以下のような図が得られることが期待できる。
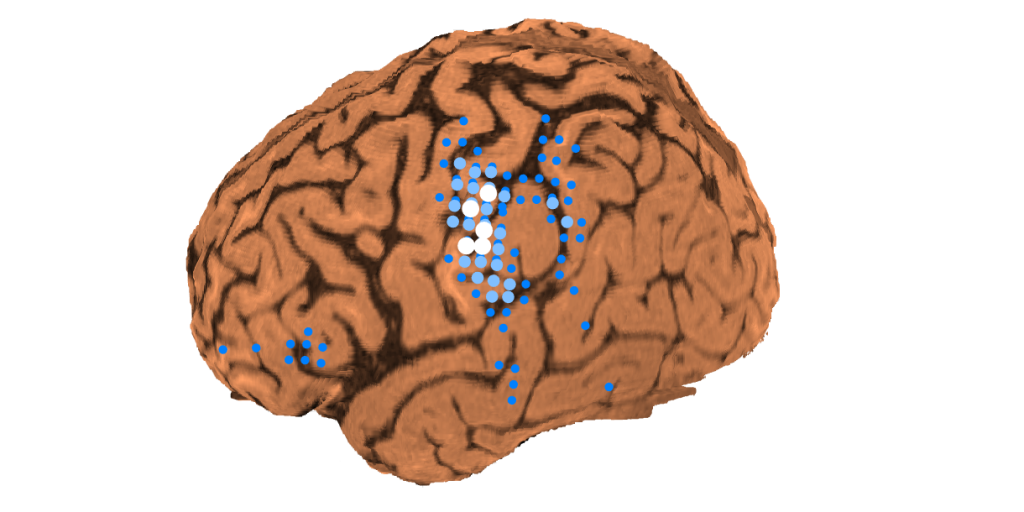
劣決定系において、測定磁場 \( \boldsymbol{b} \) と、推定磁場 \( \boldsymbol{\hat{b}}=\boldsymbol{Lq}\) は同じ値をとってしまう(常に \( \boldsymbol{b}=\boldsymbol{\hat{b}}=\boldsymbol{Lq}\), GOF=100%)ので、優決定解のような \(\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|\) を最小にすることで \(\boldsymbol{L}^{-}\) を求めることはできない。
そこで、\( \boldsymbol{b}=\boldsymbol{Lq}\) という制約の中で電流モーメント \(\boldsymbol{q}=\boldsymbol{q}_{all} \) の大きさ(ノルム)\(\|\boldsymbol{q}\|\) をできるだけ小さくなるようにすることを考える。これは数学的にはミニマムノルム解という定型的な劣決定解だ。
この場合も優決定系における最小二乗解と同様に、計算の都合上から二乗の形 \(\|\boldsymbol{q}\|^2\) にするのが常套手段だ。
$$ \boldsymbol{q}=\underset{\boldsymbol{q}}{\arg\min}\|\boldsymbol{q}\|^2 \hspace{10pt} subject \hspace{5pt}to\hspace{10pt}\boldsymbol{b}=\boldsymbol{Lq} $$
と定まる。これを解くには束縛条件の下で最適解を求める方法として、ラグランジェの未定乗数法 method of Lagrange multiplier を用いるのが常套手段だ。すなわち、ラグランジュ乗数を \(\boldsymbol{\lambda}\) として、ラグランジュ関数を \(F(\boldsymbol{q},\boldsymbol{\lambda})\) とすると、
$$ F(\boldsymbol{q},\boldsymbol{\lambda})=\|\boldsymbol{q}\|^2+\boldsymbol{\lambda}^{T}(\boldsymbol{b}-\boldsymbol{Lq})=\boldsymbol{q}^{T}\boldsymbol{q}+\boldsymbol{\lambda}^{T}(\boldsymbol{b}-\boldsymbol{Lq}) $$
\(\|\boldsymbol{q}\|^2\) が最小値をとるとき、
$$ \frac{\partial F(\boldsymbol{q},\boldsymbol{\lambda})}{\partial \boldsymbol{q}}=2\boldsymbol{q}-\boldsymbol{L}^{T}\boldsymbol{\lambda}=0 $$
$$ \frac{\partial F(\boldsymbol{q},\boldsymbol{\lambda})}{\partial \boldsymbol{\lambda}}=\boldsymbol{b}-\boldsymbol{Lq}=0 $$
これを解いて、
$$ \boldsymbol{\lambda}=2(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
$$ \boldsymbol{q}=\boldsymbol{L}^{-}\boldsymbol{b}=\boldsymbol{L}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
であり、
$$ \boldsymbol{L}^{-}=\boldsymbol{L}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-1} $$
と求まる。こうして劣決定系における逆問題の解 Inverse solution を解析的に得た。
$$ \boldsymbol{q}=\boldsymbol{L}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
この解は空間フィルターの基本的な解で、Minimum Norm Estimate (MNE) と呼ばれる [1]。MNE は必ずセンサーに近い電流双極子の電流モーメントを相対的に大きく推定してしまうので、常に脳表が光っているような解となってしまうのが欠点だ(下図)。
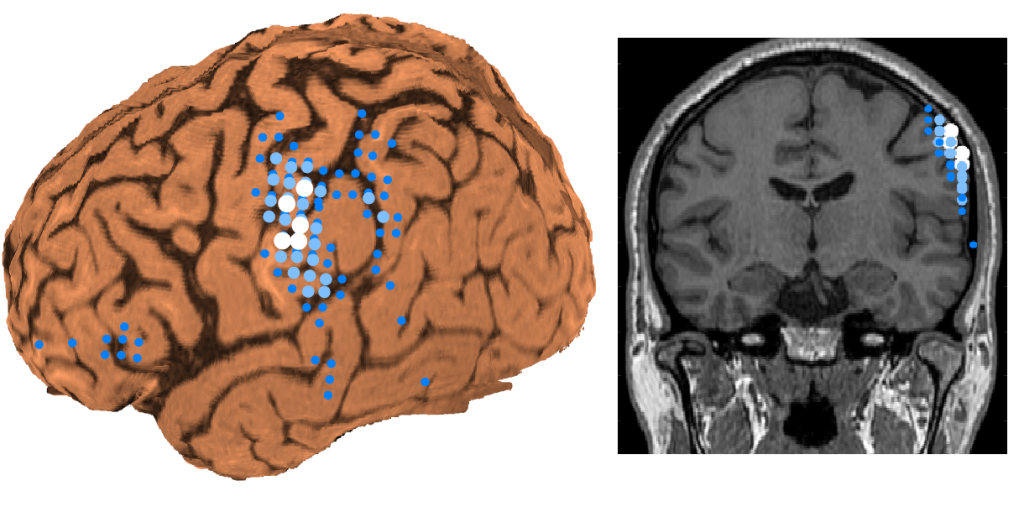
つまり、MNE 単体では脳表からある程度深部にある信号源を仮定するような状況に不向きで、脳磁図に関連した論文などでもあまり使用されていないのが実情だ。
まとめ:測定磁場 \(\boldsymbol{b}\) に対する全脳を用いた電流モーメント \(\boldsymbol{q}=\boldsymbol{q}_{all}\) の解は劣決定解であり、全脳を用いた LFM \(\boldsymbol{L}=\boldsymbol{L}_{all}\) を用いると \(\boldsymbol{q}=\boldsymbol{L}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b}\) と記述できる。
次項では、代表的な優決定解である Equivalent Current Dipole (ECD) 推定と、基本的な劣決定解である MNEを比較し、それぞれどういった状況であれば逆問題の解として採用することが正当化されるのか、それぞれの導出過程を振り返りながら検討したい。MNE を詳しく見ていくことは、空間フィルターが発展していく動機を見ていくことでもある。
(引用)
- MS Hämäläinen, RJ Ilmoniemi: Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput. 1994 Jan;32(1):35-42.