要旨:Non-adaptive Beamformer には MNE, dSPM, sLORETA, SMF などがある。
前項では、劣決定系の逆問題を解くことを、逆線形写像 \( \boldsymbol{L}^{-} \) を求めて電流モーメント \( \boldsymbol{q}\) を定めることから出発した。
$$ \boldsymbol{q}=\boldsymbol{L}^-\boldsymbol{b} $$
数学的な解はミニマムノルム推定 Minimum Norm Estimate (MNE) だが [1]、これは脳磁図解析の実情にあわないので、逆問題を解くという概念を、空間フィルターを構成することに拡張した。
こうして、重み行列 \(\boldsymbol{W}^{T}\) を求めて評価基準値 \(\boldsymbol{q}_{filtered}\) を定めることになった。
$$ \boldsymbol{q}_{filtered}= \boldsymbol{W}^T\boldsymbol{b} $$
前項より、MNE においては
$$ \boldsymbol{q}_{MNE}= \boldsymbol{q}=\boldsymbol{L}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
$$ \boldsymbol{W}^{T}=\boldsymbol{W}_{MNE}^{T}= \left(\begin{array}{cccc} \boldsymbol{L}_{1}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1} \\ \vdots \\ \boldsymbol{L}_{N}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1} \end{array} \right) =\boldsymbol{L}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1} $$
となるのであった。MNE は、その導出過程で信号全体をできるだけ小さくするよう要請しており、センサーの信号をセンサーに近い格子点だけで説明するような解が得られる。つまり、センサーに近い格子点の信号が相対的に強くなってしまう [2]。
MNEの解の分布を規定しているのは、これも前項の議論から、
$$ \frac{\|\boldsymbol{q}_{n}\|}{\|\boldsymbol{b} \|} \leq \| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F} $$
の関係であった。
最大値を標準化するには、電流モーメントをこの大きさで割って新たな評価基準をつくれば良い。この手法は Dynamic statistical parametric mapping (dSPM) とか Weight (noise) normalized minimum norm filter などと呼ばれる [3]。
$$ \boldsymbol{q}_{n_{MNE}}=\boldsymbol{q}_{n} $$
$$ \boldsymbol{q}_{n_{dSPM}}=\frac{\boldsymbol{q}_{n_{MNE}}}{\| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F}} $$
とすると、
$$ \boldsymbol{q}_{n_{dSPM}}=\frac{\boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b}}{\| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F}}=\frac{\boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b}}{\sqrt{tr(\boldsymbol{L}_{n}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-2}\boldsymbol{L}_{n})}} $$
であり、
$$ \frac{\| \boldsymbol{q}_{n_{dSPM}} \|}{\| \boldsymbol{b} \|}=\frac{\| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b}\|}{\| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F} \| \boldsymbol{b} \|} \leq \frac{\| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F}\|\boldsymbol{b}\|}{\| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F} \| \boldsymbol{b} \|}=1 $$
となる。これで各格子点の評価基準値は位置に依存せず(磁場の大きさに対する相対的な)最大値が 1 に標準化されて一定になる。このときの重み行列を \(\boldsymbol{W}_{dSPM}^{T}\) と表せば、
$$ \boldsymbol{W}_{dSPM}^{T}= \left(\begin{array}{cccc} \frac{\boldsymbol{L}_{1}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}}{\sqrt{tr(\boldsymbol{L}_{1}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-2}\boldsymbol{L}_{1})}} \\ \vdots \\ \frac{\boldsymbol{L}_{N}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}}{\sqrt{tr(\boldsymbol{L}_{N}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-2}\boldsymbol{L}_{N})}} \end{array} \right) $$
となって一件落着のように思えるが、dSPM による解は雑音が無い状態であっても信号源と位置が一致しない(位置バイアスを持つ)ことが知られている [2]。使用の際には要注意だ。
なお、dSPM の評価基準値 \(\boldsymbol{q}_{dSPM}\) の単位は、上記の式からセンサーアレイの出力単位と同じで、 fT または fT/cm だ。
ところで、分母のルート内の \( (\boldsymbol{L}\boldsymbol{L}^{T})^{-2} \) は格子点の位置に依存しないし、評価基準値 \(\boldsymbol{q}_{filtered}\) は実際の電流モーメントではなく、格子点ごとの相対的な信号強度を問題にしているのだから、\( (\boldsymbol{L}\boldsymbol{L}^{T})^{-2} \) を省略して計算量を軽くする方法が考えられる。
次の方法は dSPM の分母のルート内の \( (\boldsymbol{L}\boldsymbol{L}^{T})^{-2} \) の次数を 1 つ減らしたもので、Standardized low-resolution tomography (sLORETA)と呼ばれる [4]。
$$ \boldsymbol{q}_{n_{sLORETA}}=\frac{\boldsymbol{q}_{n_{MNE}}}{\sqrt{tr(\boldsymbol{L}_{n}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{L}_{n})}}=\frac{\boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b}}{\sqrt{tr(\boldsymbol{L}_{n}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{L}_{n})}} $$
$$ \boldsymbol{W}_{sLORETA}^{T}= \left(\begin{array}{cccc} \frac{\boldsymbol{L}_{1}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}}{\sqrt{tr(\boldsymbol{L}_{1}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{L}_{1})}} \\ \vdots \\ \frac{\boldsymbol{L}_{N}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}}{\sqrt{tr(\boldsymbol{L}_{N}^{T}(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{L}_{N})}} \end{array} \right) $$
単位について、sLORETA の評価基準値 \(\boldsymbol{q}_{sLORETA}\) の単位は、上記の式から Am となって、電流モーメントと同じだ。
さらに次の方法は dSPM の分母のルート内の \( (\boldsymbol{L}\boldsymbol{L}^{T})^{-2} \) を完全に省略し、分子の \( (\boldsymbol{L}\boldsymbol{L}^{T})^{-1} \) も省略したもので、Spatial Matched Filter (SMF)と呼ばれる [2]。
$$ \boldsymbol{q}_{n_{SMF}}=\frac{\boldsymbol{L}_{n}^{T}\boldsymbol{b}}{\|\boldsymbol{L_{n}}\|_{F}}=\frac{\boldsymbol{L}_{n}^{T}\boldsymbol{b}}{\sqrt{tr(\boldsymbol{L}_{n}^{T}\boldsymbol{L}_{n})}} $$
$$ \boldsymbol{W}_{SMF}^{T}= \left(\begin{array}{cccc} \frac{\boldsymbol{L}_{1}^{T}\boldsymbol{b}}{\sqrt{tr(\boldsymbol{L}_{1}^{T}\boldsymbol{L}_{1})}} \\ \vdots \\ \frac{\boldsymbol{L}_{N}^{T}\boldsymbol{b}}{\sqrt{tr(\boldsymbol{L}_{N}^{T}\boldsymbol{L}_{N})}} \end{array} \right) $$
単位について、SMF の評価基準値 \(\boldsymbol{q}_{SMF}\) の単位は、dSPM と同様、上記の式からセンサーアレイの出力単位と同じで、 fT または fT/cm だ。
SMF が dSPM や sLORETA と異なり興味深い点は、\(\boldsymbol{q}_{n_{SMF}}\) が直接は \(\boldsymbol{q}_{n_{MNE}}=\boldsymbol{q}_{n}\) で表現できないことだ(実際には過度に正則化すれば表現できるが)。これは結局のところ、空間フィルターにおいて重要なのは重み行列 \(\boldsymbol{W}^{T}\) を議論・提案して評価基準値の \(\boldsymbol{q}_{filtered}\) を構成することだけであり、数学的な劣決定解である MNE には最早関心がなく、優決定解のときのように推定結果を順問題で再構成することもないということで、空間フィルターを構成することと逆問題を解くことが同義となっている(下図)。
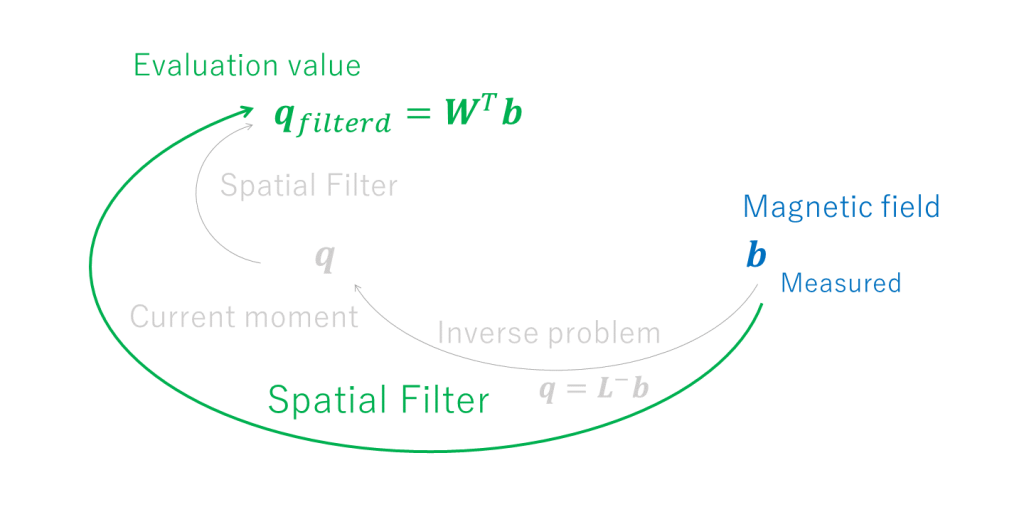
ところで、解と信号源と一致という観点から、sLORETA と SMF は雑音が無ければ位置バイアスを持たないことが知られている [2]。後述の理由で管理者は sLORETA を好む。
参考までに管理者の生理的波形(脳波の挙動からおそらくmu rhythm)を解析した結果をEquivalent Current Dipole (ECD), MNE, dSPM, sLORETA, SMF の順で示しておく。
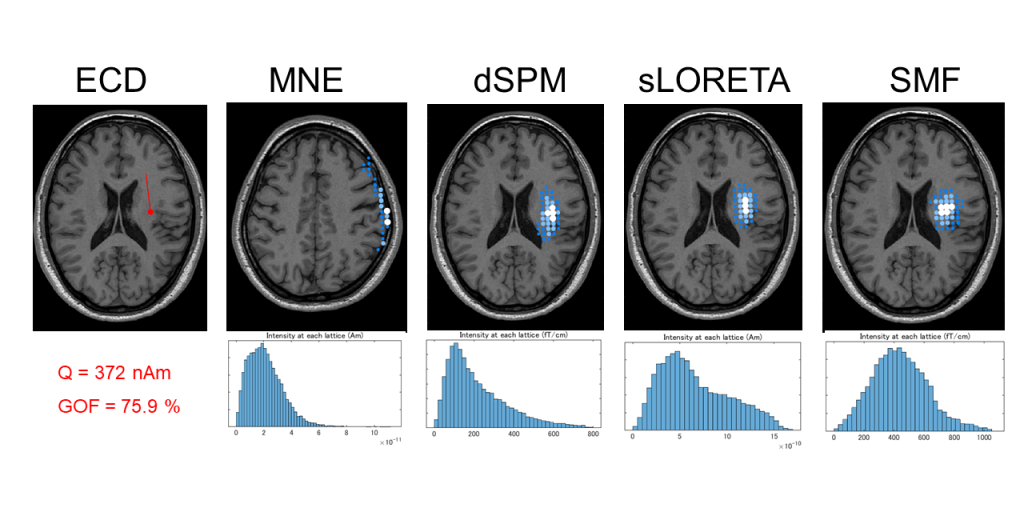
上段の ECD を除く空間フィルターは N=14,000 個の格子点に対して、信号強度(電流モーメントの大きさ)上位 100 個を示し、下段は信号強度のヒストグラムを描いた。実際には MNE を除けば画像上の解析結果はほとんど変わらない。ただし、信号強度の分布は徐々に歪みが無くなっている。
一般に信号強度の分布を、右に歪む(強い信号になるほど所属する格子点の数が急峻に少なくなる)ものほど望ましいとして評価すると、経験的にも文献的にも MNE > dSPM > sLORETA > SMF の順になる [2]。空間フィルターを構成する計算量もまた dSPM > sLORETA > SMF となる(それほど計算に時間がかかる訳ではないし、同一症例には一度計算すれば何度も適応できるが)。
なお、評価基準値の大きさは、SMF & dSPM vs. sLORETA & MNE で桁違いになっているが、これは単位に由来するものだ。
空間フィルターは信号空間全て(脳磁図解析においては脳全体)で信号が発生していると仮定しているので、非常に柔軟かつ生理的だ。
その一方でセンサーの信号数 M(=204 or 306)に比較して格子点がもたらす電流モーメントの次元数 2N(>20,000)がはるかに大きい。それゆえ空間的に高い精度は期待できないとする前提がある。こうした前提を踏まえると、急峻な分布と位置バイアスが無いことの双方を期待すると無理が生じると解釈することもできる。
どういった空間フィルターを採用するかは状況や検者の主観に委ねられるし、フィルターにより結果が大きく異なるようであれば解析対象としたサンプルが良くないのかもしれない。
個人的な好みになるが、管理者は空間フィルターなら Non-adaptive Beamformer の sLORETA を第一に採用するようにしている。理由は、
- ほどほどの計算量でストレスが無く
- 各評価基準値の単位は電流モーメントと同じであり
- 分布は比較的緩やかなので過剰に電流源の位置を制約しないが [2]
- 雑音が無ければ解が信号源と一致する(位置バイアスが無い) [2]
- Adaptive Beamformerと違い、時間幅の取り方で結果が異なることもない
からだ。
まとめ:Non-adaptive Beamformer としては様々な提案がされているが、どれも一長一短であり、運用においてはそれぞれの特徴を熟知する必要がある。
Non-adaptive Beamformer の議論に限界を感じたところで、次項では Adaptive Beamformer を検討したい。
(引用)
- MS Hämäläinen, RJ Ilmoniemi: Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput. 1994 Jan;32(1):35-42.
- Kensuke Sekihara, Maneesh Sahani, Srikantan S Nagarajan: Localization bias and spatial resolution of adaptive and non-adaptive spatial filters for MEG source reconstruction. Neuroimage. 2005 May 1;25(4):1056-67.
- AM Dale, AK Liu, BR Fischl, RL Buckner, JW Belliveau, JD Lewine, E Halgren: Dynamic statistical parametric mapping: combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron. 2000 Apr;26(1):55-67.
- RD Pascual-Marqui: Standardized low-resolution brain electromagnetic tomography (sLORETA): technical details. Methods Find Exp Clin Pharmacol. 2002;24 Suppl D:5-12.