要旨:Adaptive Beamformer は時間幅を扱うことで投入する情報量を増やし、Non-adaptive Beamformer の限界を超えることを企図する。
劣決定系の逆問題を解くことを、逆線形写像 \( \boldsymbol{L}^{-} \) を求めて電流モーメント \( \boldsymbol{q}\) を定めることから出発した。
$$ \boldsymbol{q}=\boldsymbol{L}^-\boldsymbol{b} $$
しかしながら、この数学的な解(Minimum Norm Estimate (MNE))が脳磁図解析の実情に合わないという状況に直面した。この状況を打開するために、逆問題を解くという概念を、空間フィルターを構成することに拡張した。こうして、重み行列 \(\boldsymbol{W}^{T}\) を求めて評価基準値 \(\boldsymbol{q}_{filtered}\) を定めることになった。
$$ \boldsymbol{q}_{filtered}= \boldsymbol{W}^T\boldsymbol{b} $$
ところで、そもそも順問題では、
$$ \boldsymbol{b}=\boldsymbol{Lq} $$
と表現できるのだから、
$$ \boldsymbol{q}_{filtered}= \boldsymbol{W}^T\boldsymbol{Lq} $$
と表現できるので、
$$ \boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I} $$
と単位行列になれば、
$$ \boldsymbol{q}_{filtered}= \boldsymbol{q} $$
となって評価基準値 \(\boldsymbol{q}_{filtered}\) の意味するところは電流モーメント \(\boldsymbol{q}\) に戻る。この制約条件 \(\boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I}\) のもとでより良い空間フィルターを構成すること考えたい(下図)。
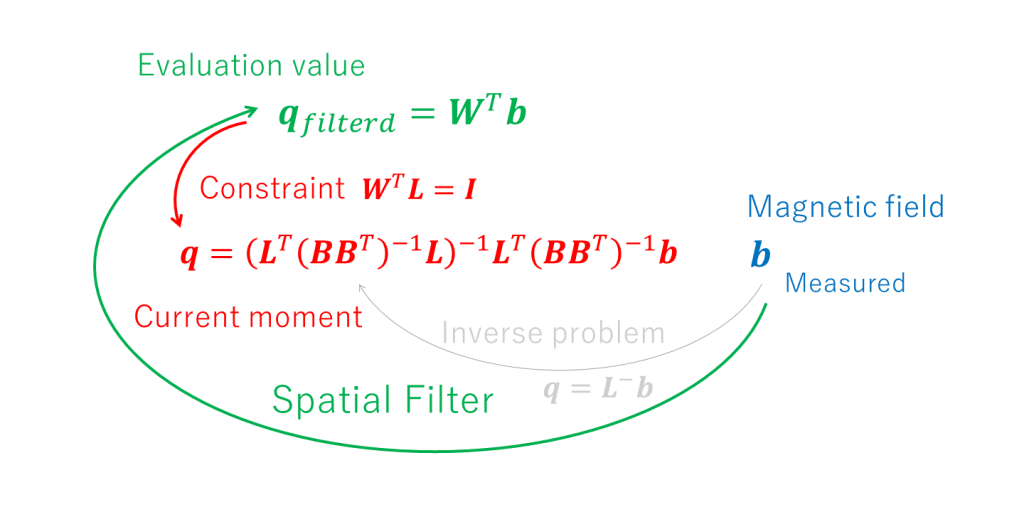
前項では、Non-adaptive beamformerとしてはMNE, dSPM, sLORETA, SMFといった様々な提案がされたが、結局のところ劣決定解の呪縛から逃れられず、どれも一長一短であり、議論に限界が感じられた。
劣決定解は情報不足の状態であり、議論の打開を企図するなら、さらに情報を投入するのが自然な解決策だ。Non-adaptive beamformer が扱っている情報は時間的な一瞬(時間軸上では 1 サンプル)に過ぎないことを考えれば、ある程度の時間幅(時間軸上では一連の複数のサンプル)を扱うようにすることが考えられる。以下では、
$$ \boldsymbol{B}=\left(\begin{array}{cccc} \boldsymbol{b}_{t=t_1} & \boldsymbol{b}_{t=t_2} & \ldots & \boldsymbol{b}_{t=t_K} \end{array} \right) $$
$$ \boldsymbol{q}_{n}^{\theta}=\left(\begin{array}{cccc} q_{n_{t=t_1}}^{\theta} & q_{n_{t=t_2}}^{\theta} & \ldots & q_{n_{t=t_K}}^{\theta} \end{array} \right) $$
$$ \boldsymbol{q}_{n}^{\phi}=\left(\begin{array}{cccc} q_{n_{t=t_1}}^{\phi} & q_{n_{t=t_2}}^{\phi} & \ldots & q_{n_{t=t_K}}^{\phi} \end{array} \right) $$
$$ \boldsymbol{Q}_{n}=\left(\begin{array}{cccc}\boldsymbol{q}_{n}^{\theta} \\ \boldsymbol{q}_{n}^{\phi} \end{array} \right) $$
のように時間 \(t=t_1,t_2, \ldots, t_K\) を考慮して検討する。
MNEを考えたときは、順問題の制約 \(\boldsymbol{b}=\boldsymbol{Lq}\) のもとで、1 サンプルなので時間幅を考慮せず、電流モーメントの大きさ \( \|\boldsymbol{q}\|^2 \) が最小になるようにした。
$$ \boldsymbol{q}=\underset{\boldsymbol{q}}{\arg\min}\|\boldsymbol{q}\|^2 \hspace{10pt} subject \hspace{5pt}to\hspace{10pt}\boldsymbol{b}=\boldsymbol{Lq} $$
今度は、先に述べたように \(\boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I}\) の制約のもとで、時間幅も考慮して、電流モーメントのパワーが最小になるようにするのが自然な拡張だ。
つまり、n 番目の格子点の \(\theta\) 方向のパワー \(\frac{1}{K}\|\boldsymbol{q}_{n}^{\theta}\|^2\) を考える(\(\phi\) 方向は同様であり、省略する)。これが最小になることを考えるのは、\(\frac{1}{K}\) を省略した \(\|\boldsymbol{q}_{n}^{\theta}\|^2=\|\boldsymbol{w}_{n}^{\theta^{T}}\boldsymbol{B}\|^2\) が最小になることを考えるのと同値なので、ここではこちらで考える(表記する)。
この手法は、Minimum Variance Spatial Filter とか、Minimum Variance Beamformer (MVBF) 、あるいは Linearly Constrained Minimum Variance Beamformer などと呼ばれる [1]。
なお、\(\frac{1}{K}\) を省略しなければ \(\frac{1}{K}\boldsymbol{BB}^{T}\) は \(\boldsymbol{B}\) の共分散行列なので、以下の式に出てくる \(\boldsymbol{BB}^{T}\) の部分は \(Cov(\boldsymbol{B})\) とか \(\boldsymbol{\Sigma}\) あるいは \(\boldsymbol{R}\) などと表記されている文献も多い。
格子点 n について \(\theta\), \(\phi\) を一括すれば \(\|\boldsymbol{Q}_{n}\|_{F}^2=\|\boldsymbol{W}_{n}^{T}\boldsymbol{B}\|_{F}^2\) を最小にすることを考えれば良い。
ただし、制約条件については \(\boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I}\) のうち \(\boldsymbol{W}_{n}^{T}\boldsymbol{L}_{n}=\boldsymbol{I}_{2}\) の情報しか使用せず(必要条件となり)、対角成分とその前後以外の条件は使用しないことになる。したがって、後で制約条件が満たされているか(\(\boldsymbol{W}^T\boldsymbol{L}\)が単位行列に近いか)評価が必要になる。
$$ \boldsymbol{W}_{n}^{T}=\underset{\boldsymbol{W}_{n}^{T}}{\arg\min}\|\boldsymbol{W}_{n}^{T}\boldsymbol{B}\|_{F}^2 \hspace{10pt} subject \hspace{5pt}to\hspace{10pt}\boldsymbol{W}_{n}^{T}\boldsymbol{L}_{n}=\boldsymbol{I}_{2} $$
MNE の解法と同様、ラグランジェの未定乗数法 method of Lagrange multiplier を用いる。すなわち、ラグランジュ乗数を \(\boldsymbol{\Lambda}\) として、ラグランジュ関数を \(F(\boldsymbol{W}_{n}^{T},\boldsymbol{\Lambda})\) とすると、
$$ F(\boldsymbol{W}_{n}^{T},\boldsymbol{\Lambda})=tr(\boldsymbol{W}_{n}^{T}\boldsymbol{BB}^{T}\boldsymbol{W}_{n}-(\boldsymbol{W}_{n}^{T}\boldsymbol{L}_{n}-\boldsymbol{I}_{2})\boldsymbol{\Lambda}) $$
\(\|\boldsymbol{Q}_{n}\|_{F}^2=\|\boldsymbol{W}_{n}^{T}\boldsymbol{B}\|_{F}^2\) が最小値をとるとき、
$$ \frac{\partial F(\boldsymbol{W}_{n}^{T},\boldsymbol{\Lambda})}{\partial \boldsymbol{W}_{n}^{T}}=2\boldsymbol{W}_{n}^{T}\boldsymbol{BB}^{T}-\boldsymbol{\Lambda}^{T}\boldsymbol{L}_{n}^{T}=\boldsymbol{O} $$
$$ \frac{\partial F(\boldsymbol{W}_{n}^{T},\boldsymbol{\Lambda})}{\partial \boldsymbol{\Lambda}}=(\boldsymbol{W}_{n}^{T}\boldsymbol{L}_{n}-\boldsymbol{I}_{2})^{T}=\boldsymbol{O} $$
から、
$$ \boldsymbol{W}_{n}^{T}=\frac{\boldsymbol{\Lambda}^{T}}{2}\boldsymbol{L}_{n}^{T}(\boldsymbol{BB}^{T})^{-1} $$
だから、
$$ \boldsymbol{W}_{n}^{T}\boldsymbol{L}_{n}=\frac{\boldsymbol{\Lambda}^{T}}{2}\boldsymbol{L}_{n}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L}_{n}=\boldsymbol{I}_{2} $$
となって、
$$ \boldsymbol{\Lambda}^{T}=2(\boldsymbol{L}_{n}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L}_{n})^{-1} $$
$$ \boldsymbol{W}_{n}^{T}=(\boldsymbol{L}_{n}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L}_{n})^{-1}\boldsymbol{L}_{n}^{T}(\boldsymbol{BB}^{T})^{-1} $$
と求まる。なお、
$$ \boldsymbol{W}^{T}=\underset{\boldsymbol{W}^{T}}{\arg\min}\|\boldsymbol{W}^{T}\boldsymbol{B}\|_{F}^2 \hspace{10pt} subject \hspace{5pt}to\hspace{10pt}\boldsymbol{W}^{T}\boldsymbol{L}=\boldsymbol{I} $$
でも解法は \( \boldsymbol{W}_{n}^{T}\to\boldsymbol{W}^{T} \), \(\boldsymbol{L}_{n}\to\boldsymbol{L}\), \(\boldsymbol{I}_{2}\to\boldsymbol{I}\) とすれば同様であり、
$$ \boldsymbol{\Lambda}^{T}=2(\boldsymbol{L}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L})^{-1} $$
$$ \boldsymbol{W}^{T}=(\boldsymbol{L}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L})^{-1}\boldsymbol{L}^{T}(\boldsymbol{BB}^{T})^{-1} $$
となって直接 \( \boldsymbol{W}^{T}\) が求まる。実際、van Veen 論文でもこのような表現となっている [1]。
とはいえ実際の解析となると、\((\boldsymbol{L}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L})^{-1}\) は 2Nx2N(管理者の脳なら28,000×28,000)の \(\boldsymbol{L}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L}\) から逆行列を求めるので大変だ。
それが嫌で重み行列 \(\boldsymbol{W}^{T}\) の数値として成分 \(\boldsymbol{W}_{n}^{T}\) を求める手法を用いた場合、制約条件 \(\boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I}\) の一部(を必要条件として)しか用いていない。計算上は 2Nx2N の単位行列のうち、対角成分とその前後以外は条件として用いていない。各重みベクトルと任意のリードフィールドベクトルが常に独立なら、\(\boldsymbol{l}_{n}^{\theta}\) 以外の任意のリードベクトルを \(\boldsymbol{l}_{k}^{\omega}\) とすると、制約条件 \(\boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I}\) の対角成分以外は
$$ \boldsymbol{w}_{n}^{\theta^{T}}\boldsymbol{l}_{k}^{\omega}=0 $$
のように全て0となって良いのだが、そうはならないことが強く予想される(2N=28,000個の重みベクトル各々に対して2N-1=28,000-1個のリードベクトル全てが常に独立というのは現実的でない)ので、\(\boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I}\) の対角成分以外がどうなっているのか評価が必要だ。
その一方で、直接 \( \boldsymbol{W}^{T}\) を求めた場合は逆行列 \((\boldsymbol{L}^{T}(\boldsymbol{BB}^{T})^{-1}\boldsymbol{L})^{-1}\) を求めるために(やはり 2N=28,000 全てのベクトルが各々独立というのは現実的でないので)計算上の工夫が必要だ。
このあたりは結局同じことを問題にしているので、どちらの手法が良いというわけではないのだろうけれども、計算量節約のために普通は \(\boldsymbol{W}_{n}^{T}\) を求めて \(\boldsymbol{W}^T\boldsymbol{L}=\boldsymbol{I}\) の対角成分以外を評価するのが一般的なようだ。
ところで、めでたく \(\boldsymbol{W}^{T}\) を構成して(何も考えずに)解析に適応すると、下図のようになる
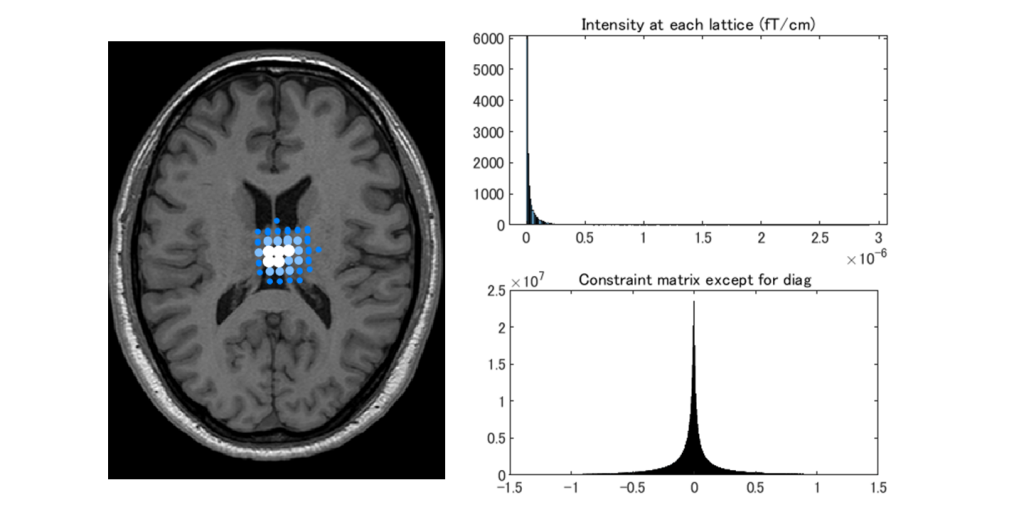
右上の信号強度(電流モーメントの大きさは)の分布(ヒストグラム)は急峻に右に歪んだし(上位 5 つは順に 2,922 nAm, 1,725 nAm, 1,521 nAm, 1,286 nAm, 1,225 nAm)、右下の制約条件の左辺から右辺を引いた \(\boldsymbol{W}^T\boldsymbol{L}-\boldsymbol{I}\) の各成分についてのヒストグラムから制約条件 \(\boldsymbol{W}^T\boldsymbol{L}\) は単位行列に近くなっていると言える。しかし、解析結果は脳の中心を指している。あれこれと試してどのサンプルを選ぼうと、MVBFを単純に適応すると脳の中心が光る絵しか得られない。
脳磁図解析の基礎となっている Sarvas 式の性質から、仮想球中心(脳の中心)では電流双極子は磁場を発生しない(リードフィールド \(\boldsymbol{L}_{n}\) の全ての成分がゼロ)なので、制約条件 \(\boldsymbol{W}_{n}^T\boldsymbol{L}_{n}=\boldsymbol{I}\) を満たす重み \(\boldsymbol{W}_{n}^{T}\) の全ての成分は無限大に発散してしまう。こうなるとせっかく制約条件が成立するようにしても
$$ \boldsymbol{q}_{n}=\boldsymbol{W}_{n}^{T}\boldsymbol{b} $$
も無限大に発散してしまう。つまり、脳の中心近傍では解析にならない。
Non-adaptive Beamformer の MNE では常に脳表が光る絵しか得られなかったことと対照的とも言えるが、サンプルにかかわらず中心しか光らないようでは解析とは言えず、結果は MNE よりも悪い。使い物にならない。
このように MVBF は良いアイデアなのだが、脳磁図解析の基礎となる Sarvas 式の性質に由来して、単純に適応すると必ず失敗してしまう。
まとめ:Adaptive BeamformerであるMVBFは、脳磁図解析に単純に適応すると使い物にならない。
次項では、MVBFを現実的な解析に適応させるための工夫について検討したい。
(引用)
- BD van Veen, W van Drongelen, M Yuchtman, A Suzuki: Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Trans Biomed Eng. 1997 Sep;44(9):867-80.