要旨:脳磁図解析の基本となる Sarvas 式を確認する。
Sarvas formula は電流双極子の概念を導入して球対称な導体を仮定することで得られる Biot-Savart law の解析解だ [1]。
これにより任意の座標における磁場が、積分計算を使わず、行列計算のみで導出可能となった。
Sarvas論文の要旨は、
- Biot-Savart 式を、Maxwell 方程式とベクトル解析を用いて変換していく
- まず、均一で境界の無い導体について議論をし
- 次に、(等価)電流双極子 equivalent current dipole (ECD) の概念を導入する
- さらに、不均一で境界を有する導体について議論をして、
- 球対称な場合のSarvas式を得る
といったもので、結局用いている仮定は、
Maxwell 方程式、電流双極子の概念、球対称な導体
の3つだ。脳磁図解析で中心座標を必要とするのは、この球対称な導体を仮定しているからだ。
以下に Sarvas 式を示す。なお、原著では磁場 \(\boldsymbol{B}\) としているが、任意の場所における磁場はベクトルなので、磁場 \(\boldsymbol{b}\) とした。同様に、電流モーメント \(\boldsymbol{Q}\) は電流モーメント \(\boldsymbol{q}\) とした。
球対称な不均一で境界を有する導体を考える。
仮想球中心を位置の原点 \(\boldsymbol{O}\) とする。電流モーメント \(\boldsymbol{q}\) の電流双極子が位置 \(\boldsymbol{r_0}\) にあるとき、位置 \(\boldsymbol{r}\) における磁場 \(\boldsymbol{b}\) を考える。
ただし、真空の透磁率を \(\mu_0\) とし、すべての位置において透磁率は \(\mu_0\) に等しいものとする。
Sarvas式はこの条件の下で以下の解析解を与える。
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi F^2}(F\boldsymbol{q}\times\boldsymbol{r_0}-\boldsymbol{q}\times\boldsymbol{r_0}\cdot\boldsymbol{r}\boldsymbol{\nabla}F) $$
ただし、
$$ \boldsymbol{\nabla}F=(r^{-1}a^2+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r}+2a+2r)\boldsymbol{r}-(a+2r+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r})\boldsymbol{r_0} $$
$$ F=a(ra+r^2-\boldsymbol{r_0}\cdot\boldsymbol{r}),\hspace{10pt}\boldsymbol{a}=\boldsymbol{r}-\boldsymbol{r_0},\hspace{10pt}a=|\boldsymbol{a}|,\hspace{10pt}r=|\boldsymbol{r}| $$
各ベクトルについて図示すると以下のようになる。
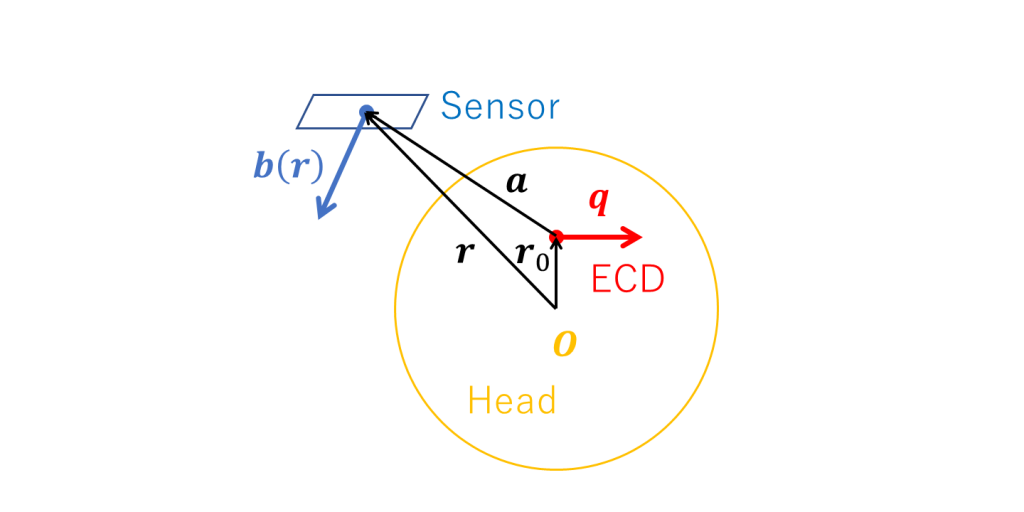
まとめ:Sarvas 式は、わずかな仮定から Biot-Savart law の解析解として得られる。
次項では、この Sarvas 式を用いて脳磁図解析における原則を確認したい。
(引用)
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.