要旨:センサーアレイから得られる情報量に対する電流源の相対的な情報量により、得られる解は優決定解と劣決定解に大別される
逆問題を解くことは磁場から電流モーメントを推定することだが、その前に双方の情報量を評価しておく必要がある。
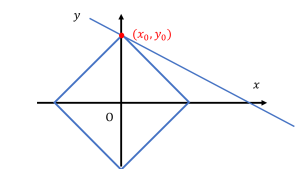
情報量が 2 対 2 の場合、例えば中学校で習う 2 次元連立方程式なら、下図のように与えられた 2 本の線から成分を 2 つ持つ交点 \((x_{0},y_{0})\) を導くという数学的に「適切な」解法が適応できる。
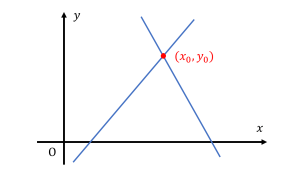
しかしながら、脳磁図解析においては得られた情報の数と求める解の数が合わない「不適切な」状況が起こっている。具体的には単一電流双極子法なら情報量は 5 対 204 というのが代表的だ。
センサーアレイから出力される信号(情報)の数はセンサー数 M=306 or less だ。管理者の場合、平時は planar gradiometers を全て採用しているから M=204 となる。
一方で電流源の持つ情報の数はどうだろうか?
まず、単一電流双極子法の場合を考える [1]。この場合、電流モーメントの位置は \(r_{x}\), \(r_{y}\), \(r_{z}\) の 3 つ情報と、電流の成分 \(q_{\theta}\), \(q_{\phi}\) の 2 つの情報を持つ。つまり単一電流双極子の持つ情報量は 5 つであり、これはセンサーアレイが出力する情報の数より圧倒的に少ない。電流双極子が数個に増えても状況は同じだ。
この情報過多な状態を数学的には優決定系 overdetermined system という。優決定系の解法として、与えられた情報のバランスを取る妥協点を探ることが考えられる。
模式的に連立方程式が3本与えられた場合に妥協点 \((x_{0},y_{0})\) を求めることを考える。これら3 本の線の交点というものは存在しない(情報として矛盾している)が、3 本の線で囲まれた領域の真ん中あたりが妥協点としてある程度の説得力があると考えられる。
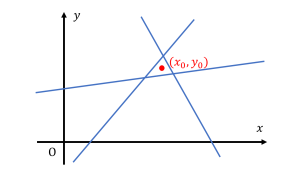
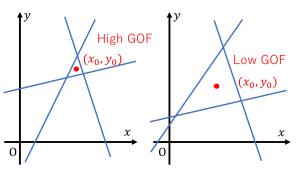
そしてその「説得力」は点の選び方よりもむしろ、どういった 3 本の線を採用するかによって決まってくることもわかる。脳磁図においてこの説得力は当てはまりの良さ goodness of fit (GOF)と呼ばれる。そして説得力を上げるためには、与えられた情報から採用する情報を吟味することも時に有効であることがわかる(センサーの選択)。
次に、空間フィルター法(格子状に並んだ電流双極子が脳全体を埋め尽くす)の場合を考える。各電流双極子は 5 つの情報を持っており、格子点の数だけ電流双極子が存在するので(管理者の大脳は 5mm 幅の格子点 14,000 個程度)、センサーアレイが出力する情報の数は電流双極子群が持つ情報の数よりも圧倒的に少ない。
この情報不足な状態を数学的には劣決定系 underdetermined system という。劣決定系の解法として、与えられた情報の中から条件を満たすものだけを取り出すことが考えられる。
模式的に連立方程式が 1 本与えられた場合に解 (x0,y0) を求めることを考える。1 本の線の上ならどこでも解になるのだが、原点からできるだけ近いものだけを解とする、と決めてしまえば内接円の接点が解となることがわかる((L2) minimum norm estimate [2])。
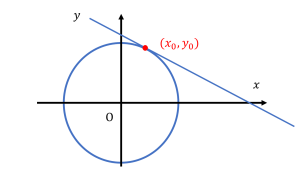
そして条件の決め方は全くの任意であり、例えば内接する正方形でも構わない (L1 minimum norm estimate [3])。
条件は様々提案されているけれどもどの方法も一長一短であり、状況に応じて適切な方法を使っていくことになる。
まとめ:逆問題の解は相対的な情報量により優決定系と劣決定系に大別される。
次項では、まず優決定系について考えていきたい。
(引用)
- E Kaukoranta, M Hämäläinen, J Sarvas, R Hari: Mixed and sensory nerve stimulations activate different cytoarchitectonic areas in the human primary somatosensory cortex SI. Neuromagnetic recordings and statistical considerations. Exp Brain Res. 1986;63(1):60-6.
- MS Hämäläinen, RJ Ilmoniemi: Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput. 1994 Jan;32(1):35-42.
- Uutela K, Hämäläinen M, Somersalo E. Visualization of magnetoencephalographic data using minimum current estimates. Neuroimage. 1999 Aug;10(2):173-80.