要旨:脳磁計が磁場を測定することで議論できる電流には最小単位がある
前項では電流双極子の概念を導入し、電流モーメントという電流を表すベクトル量を持ち、単位は Am ということを述べた。また、電流双極子は点であり、位置を持つことも述べた。
これにより脳内の電流を点電流として簡便に(電流の空間的な広がりを考慮せずに)議論することができるようになった [1]。
脳磁計による電流の測定において、その最小単位としては 10 nAm が要求される、と伝統的に信じられている [2]。これは実験的に決めた値というよりは、計算した結果をグラフにプロットした結果だ。
以下の図は一般的な測定条件の例として、管理者の脳で仮想実験している。順問題は Sarvas 式を用い [1]、半径 7 cm の仮想球を呈する脳表において、センサーは仮想球中心に対して水平に固定されており、脳表からセンサーへの距離は3 cmと仮定する。また、planar gradiometer / axial gradiometer それぞれの接合距離(baselineと称する)は 1.68 / 3 cmと仮定する。
脳表から 1 cm の深さに10 nAm の電流が planar gradiometer の差分と垂直方向かつ脳表と水平方向(x 軸方向)に流れていると仮定する。センサーの反応を見るために電流を動かすのだが、電流双極子は電流に垂直な平面(yz 平面)を、仮想球中心に対して点 (0, 6, 0) から始まり (0, 0, 6) を通り (0, -6, 0) に至る半円運動するものとする。
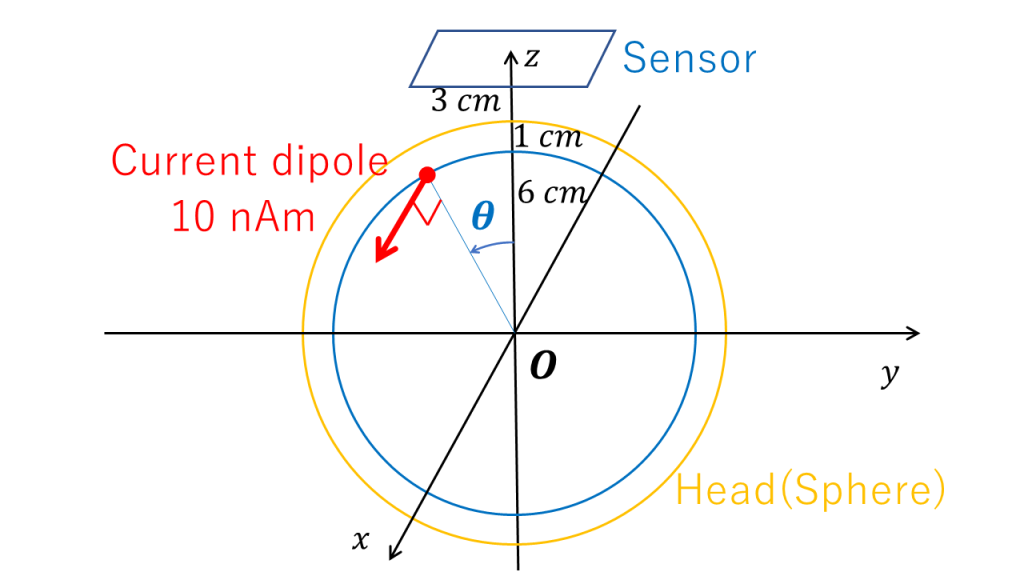
そうすると下図のようなグラフが得られる。
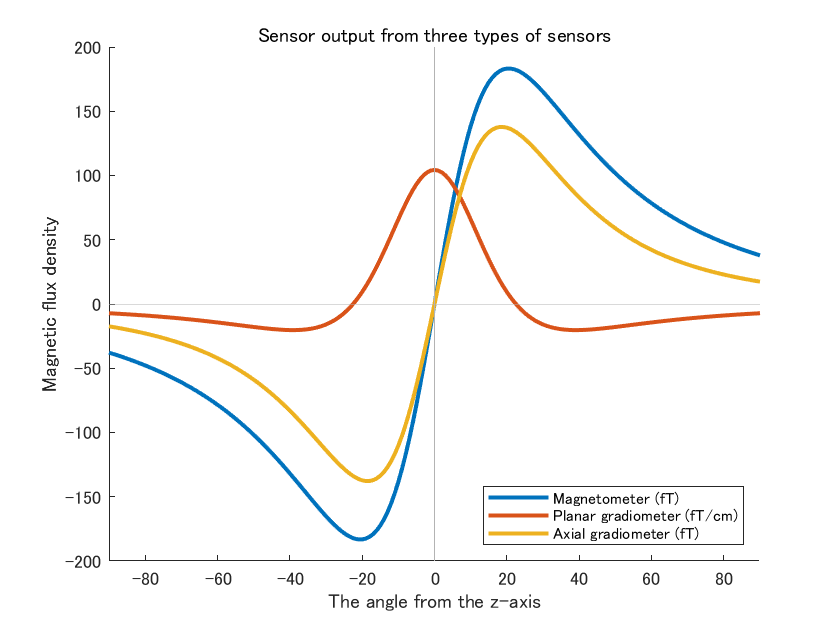
実臨床において 200 fT とか 100 fT/cm 程度であれば波形を視認できる下限と言えるから、一般的な測定条件で 10 nAm は検出可能な単位だと考えることができる。
なお、Hämäläinen の総説 Fig 27 とほぼ同一のグラフが欲しければ [2]、仮想球半径 10 cm、脳表からセンサーへの距離 0.25 cm(未記載)、planar gradiometer / axial gradiometer それぞれの接合距離は 1.36(本文中は 1.5 cm と記載) / 6 cm、電流の深さ 3 cm として、planar gradiometerの出力を接合距離で割らずに単位を fT にしてしまえば良い(下図)。
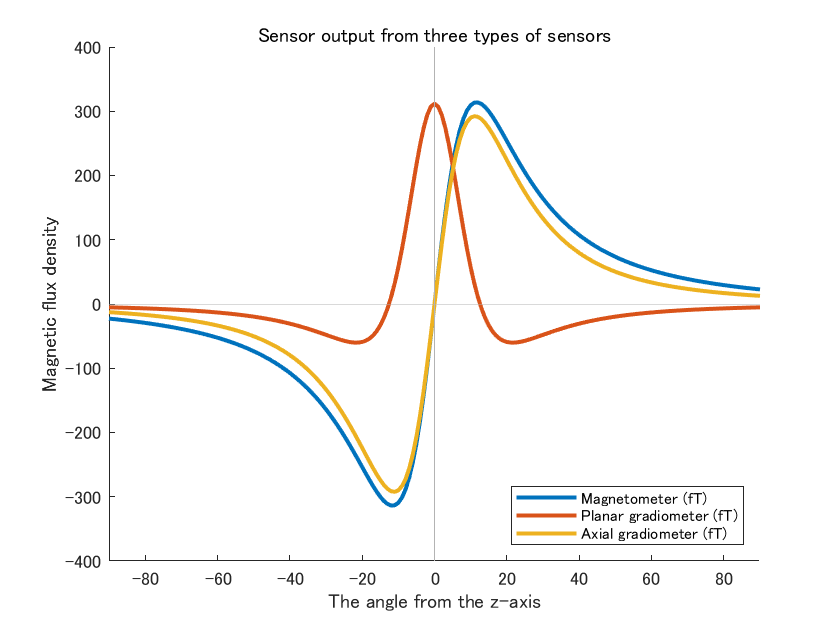
ただ、脳表からセンサーへの距離が近接し過ぎて現実離れしてしまっており、そのためか当該の論文中には「半球表面で測定している」と記載してあるのみで、センサー・脳表間の具体的な距離の記載が無い。加えて、半径 10 cm の脳といえば体積にして4,200 mL であり、管理者の脳(半径 7 cm)の体積 1,400 mL の 3 倍にあたる。どうしてこんな数字を採用したのか不明だが、わかりやすい図をつくるためにこうした仮想的な状況を想定したのだろう。
蛇足ながら、これらのグラフから、magnetometer / axial gradiometer においてはセンサー直下に電流があるとセンサー出力はゼロになることがわかる。これは強い出力を示すセンサーの直下には測定を企図している電流が無いということでもある。そのために等磁場線図を描いてセンサー出力の正負の谷を形成するゼロのラインを探すことが要求され、それでようやく測定を企図する電流の位置が推測できるということになる。
こうしたセンサー出力の複雑なふるまいは、脳磁図の直感的な理解を妨げ、初学者を遠ざけてきたものだと管理者は考える。
まとめ:脳磁計による電流の測定で要求される最小単位は、一般的な測定条件ならば達成可能である
次項では、電流モーメントの最小単位である10 nAmを起こすのに必要な大脳皮質の面積について議論したい。
(引用)
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.
- MS Hämäläinen, R Hari, RJ Ilmoniemi, J Knuutila, OV Lounasmaa: Magnetoencephalography theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993 Apr;65(2):413-97.