要旨:脳磁図で電流を議論するために、電流双極子と呼ばれる概念を導入する
前項では、脳が発する磁場の発生源となる細胞内電流について議論した。
しかし脳は脳表だけに限っても様々な形状の脳溝を形成するなど構造は複雑だ(下図は管理者の脳)。
しかも発生源である錐体細胞の大脳皮質における密度は 10万個\( /mm^2\)と非常に高く [1]、密度や皮質の厚さは場所によりバラツキもある。対象が病的な脳であればさらに複雑さとバラツキ具合が増す。この複雑な構造と、膨大な数の電流源を簡便に扱うことを考えたい。
これには、関心となる空間において全ての微小な電流を足し合わせることで得られる総和的概念が良いだろう。そして足し合わせる対象は、単に電流(単位は \( A \) )だとスカラー量であり総和には不向きであり、向きも考慮したベクトル量である電流密度(単位は \( A/m^2 \) )が良いだろう。
また、関心となる空間の体積は状況に応じて異なるのだから、この概念自体には体積を考慮せずに済むよう、点としての性質が望ましいだろう。そして前項の議論から、こうした電流の総和的概念に点電流としての性質をもたせることは、顕微鏡レベルの解剖学から十分に合理的と言えるだろう。
この概念は、(等価)電流双極子 equivalent current dipole (ECD) と呼ばれる。電流の大きさと向きを表す電流モーメントというベクトル量を持ち、その単位は
$$ Am (= (A/m^2) \cdot (m^3)) $$
だ。また、電流双極子は位置を持つが、点であり、体積を持たない。
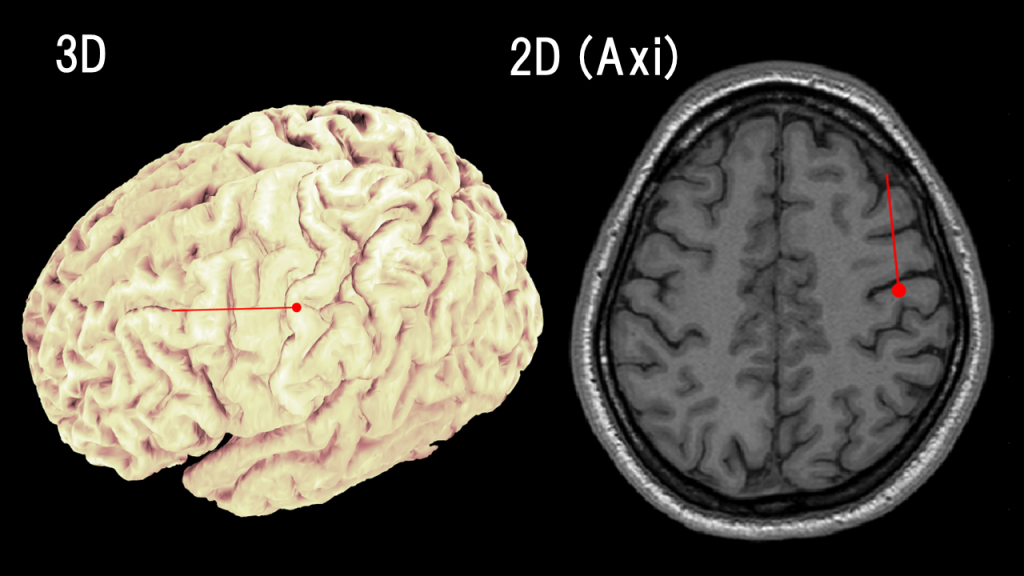
電流双極子はマチ針で脳画像に重畳されるのが慣例で、マチ針の頭の部分で位置を、針の向きと大きさで電流モーメントの向きと大きさを表す。
そして ECD 推定をするなどして電流双極子が任意の位置に出現することを、これも慣例として「~にダイポールが立つ」などと表現する(下図は管理者の脳に生理的な活動で ECD 推定をしたもの)。
電流双極子は、ある三次元領域の電流密度(細胞内電流)\( \boldsymbol{j}_i \) を一点(位置 \( \boldsymbol{r}_0 \))に集中したもの、と定義され、数式では以下のように導出される [2]。
三次元領域 \( G \) における電流密度 \( \boldsymbol {j}(\boldsymbol {r}’) \) より生じる位置 \( \boldsymbol{r} \) における磁場 \( \boldsymbol{b}(\boldsymbol{r}) \) は Biot–Savart の法則から、前項での議論のごとく体積電流が無視できる状況において
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’ $$
と表されるが、体積積分は煩雑なので、これを簡便に表現したい。
まず、脳磁計が測定を企図している脳皮質の範囲がごく小さいこと、すなわち三次元領域 \( G \) が微小であることを利用する。
次に、センサーが頭皮・頭蓋骨を隔てて常に脳の外にあること、すなわち三次元領域 \( G \) における任意の位置 \( \boldsymbol{r}’ \) がセンサーの位置 \( \boldsymbol{r} \) から十分に離れていることを利用する。
上記の仮定が成立する状況において、微小な三次元領域 \( G \) のある位置(例えば中心)を \( \boldsymbol{r}_0 \) と表現すれば、\( \boldsymbol{r}-\boldsymbol{r}’\simeq\boldsymbol{r}-\boldsymbol{r}_0 \) と近似できるから、
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’\simeq \frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’) dv’\times\frac{\boldsymbol{r}-\boldsymbol{r}_0}{|\boldsymbol{r}-\boldsymbol{r}_0|^3} $$
と外積の計算を体積積分の外に出すことができる。そこで
$$ \boldsymbol{q}= \int_G \boldsymbol {j}_i(\boldsymbol {r}’) dv’ $$
と電流モーメントを定義すれば、
$$ \boldsymbol{b}(\boldsymbol{r})\simeq \frac{\mu_0}{4\pi}\boldsymbol{q}\times\frac{\boldsymbol{r}-\boldsymbol{r}_0}{|\boldsymbol{r}-\boldsymbol{r}_0|^3} $$
となる。Dirac delta 関数 \( \delta (\boldsymbol{r}) \) を用いて
$$ \boldsymbol{j}_i (\boldsymbol{r})= \delta (\boldsymbol{r}-\boldsymbol{r}_0) \boldsymbol{q} $$
と定義すると、
$$ \int_G \boldsymbol {j}_i(\boldsymbol {r}’) dv’=\int_G \delta (\boldsymbol{r}’-\boldsymbol{r}_0) \boldsymbol{q} dv’=\boldsymbol{q} $$
と表現できる [2]。
このように電流双極子の概念は Sarvas 式を導出する過程において、煩雑な体積積分を回避している。それゆえ、電流双極子の概念を受け入れて Sarvas 式を順問題の解として採用することは、脳磁図解析における計算処理が高速化することを意味する。
当然ながら、電流双極子は微小な領域の電流を表現することが前提となっているので、ある程度の大きさを持つ領域の電流を議論するなら、近似の妥当性を評価するか、複数の電流双極子を想定する必要がある。
まとめ:電流双極子の概念を導入した。電流双極子は電流モーメントという電流の大きさと向きを表すベクトル量を持ち、点であるから位置を持つ一方で、体積は持たない
次項では、脳磁図における電流モーメントの最小単位は10 nAm が要求されていること、またその根拠について議論したい。
(引用)
- MS Hämäläinen, R Hari, RJ Ilmoniemi, J Knuutila, OV Lounasmaa: Magnetoencephalography theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993 Apr;65(2):413-97.
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.