Abstract: Depending on the relative amount of information from the current source and the sensor array, inverse solution types can be broadly classified into overdetermined and underdetermined systems.
Solving the inverse problem involves estimating the current from the magnetic field. However, before that, it is necessary to evaluate the amount of information in both.
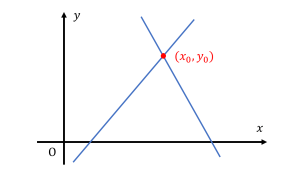
For example, when the amount of information is balanced—such as in a two-dimensional system of simultaneous equations commonly taught in junior high school—we can find the intersection point (with two components) of two given lines, as illustrated in the figure below. This allows us to obtain a mathematically “appropriate” solution \((x_{0},y_{0})\).
However, in magnetoencephalography analysis, the situation is often “inappropriate” because the amount of information obtained does not match the number of possible solutions. For example, a single current dipole has 5 pieces of information, while the planar gradiometers provide 204 signals.
The sensor array outputs up to 306 signals, with 204 signals coming from the planar gradiometers. On the other hand, how much information is provided by the current source?
First, we consider the single current dipole estimation [1]. In this method, the dipole has three positional components \(r_{x}\), \(r_{y}\), and \(r_{z}\), and two current moment components, \(q_{\theta}\) and \(q_{\phi}\). In other words, a single current dipole provides five pieces of information, which is far less than the information output by the sensor array. This imbalance remains even if the number of current dipoles increases to several.
The situation described above, where there is an information overload, is called an overdetermined system mathmatically. One way to solve such an overdetermined system is to find a compromise that balances the available information.
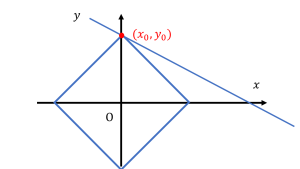
Let’s consider a schematic example below in which we are given three simultaneous equations to find a compromise point \((x_{0},y_{0})\). The intersection of the three lines does not exist (in other words, the information is contradictory), but the center of the area enclosed by the three lines can be considered a reasonable compromise point.
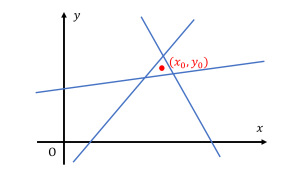
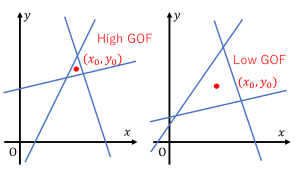
We can see that the “reasonableness” depends not on how the points are selected, but on which three lines are chosen. In MEG, this reasonableness is referred to as the goodness of fit (GOF). To improve reasonableness, it is also effective to carefully consider which information to use from the available data (i.e., sensor selection).
Next, we consider the spatial filter, in which each current dipoles arranged on each grid fill the entire brain. Each current dipole has five components of information, and there are as many current dipoles as grid points. For example, the administraiter’s brain contains approximately 14,000 grid points at a spacing of 5 mm. Therefore, the amount of information output by the sensor array is vastly lower than the information held by the current dipoles.
The situation described above, where there is a lack of information, is called an underdetermined system mathematically. One approach to solving such an underdetermined system is to extract only the information that satisfies a given constraint.
Let’s consider a schematic example below in which we are given a single equation and are trying to find a solution \((x_{0},y_{0})\). Any point on the line can be a solution, but if we restrict ourselves to the point closest to the origin, we find that the tangent point of the inscribed circle provides the solution ((L2) minimum norm estimate [2]).
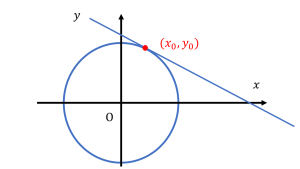
And the constraint can be chosen arbitrarily. For example, an inscribed square can be used (L1 minimum norm estimate [3]).
Various constraints have been proposed, but each method has its advantages and disadvantages, so the appropriate method should be selected based on the specific situation.
Summary: Inverse solution types can be broadly classified into overdetermined and underdetermined systems depending on the relative amount of information.
In the next page, I would like to discuss the overdetermined system.
(References)
- E Kaukoranta, M Hämäläinen, J Sarvas, R Hari: Mixed and sensory nerve stimulations activate different cytoarchitectonic areas in the human primary somatosensory cortex SI. Neuromagnetic recordings and statistical considerations. Exp Brain Res. 1986;63(1):60-6.
- MS Hämäläinen, RJ Ilmoniemi: Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput. 1994 Jan;32(1):35-42.
- Uutela K, Hämäläinen M, Somersalo E. Visualization of magnetoencephalographic data using minimum current estimates. Neuroimage. 1999 Aug;10(2):173-80.