Abstract: ECD estimation assumes only one grid point, which is far fewer than the number of sensors. Hence, the inverse solution can be obtained formulaically and analytically in the overdetermined system.
According to the Sarvas formula, the forward solution, once the position of the current dipole is determined, a linear correspondence (linear mapping) is established between the current moment \( \boldsymbol{q} \) and the magnetic field \( \boldsymbol{b} \), and this correspondence (mapping) is called the Lead Field Matrix (LFM).
In other words, if we introduce LFM as \( \boldsymbol{L} \), it can be expressed in the form of a matrix operation as follows:
$$ \boldsymbol{b}=\boldsymbol{L}\boldsymbol{q} $$
Now we would like to find the inverse linear correspondence (inverse linear mapping) \(\boldsymbol{L}^{-}\) that estimates the current moment from the magnetic field as follows:
$$ \boldsymbol{q}=\boldsymbol{L}^-\boldsymbol{b} $$
This is called the inverse problem (see figure below).
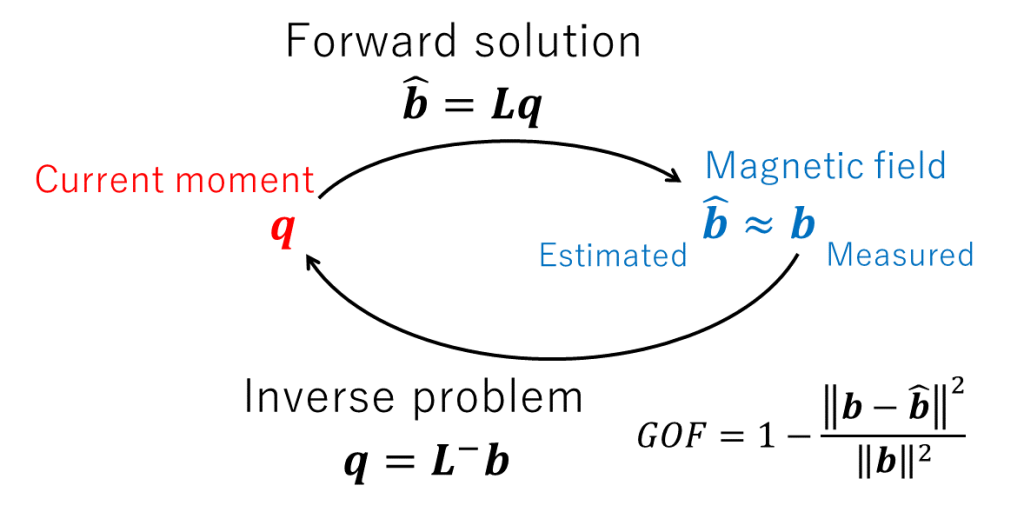
As discussed in the forward solution, assuming the number of sensor arrays is M, the number of lattice points is N, and the number of points constituting the LFM is \(N_{LFM}\), then \(\boldsymbol{b}\) is an M-dimensional column vector, \(\boldsymbol{q}\) is a \(2N_{LFM}\)-dimensional column vector, and \( \boldsymbol{L} \) is a matrix of \( M\times2L_{LFM} \).
The situation where \(M>2N_{LFM}\) is called an overdetermined system, which is a state of information overload. The single-dipole estimate has the situation of M=204 or 306 whereas \(N_{LFM}=1\), which is a typical overdetermined solution.
In the following, let us consider estimating the current moment \( \boldsymbol{q} \) in the n-th lattice point. We immediately get \(N_{LFM}=1\) and the followings:
$$ \boldsymbol{L}=\boldsymbol{L}_{n}=\left(\begin{array}{cccc}\boldsymbol{l}_{n}^\theta &\boldsymbol{l}_{n}^\phi \\\end{array}\right) $$
$$ \boldsymbol{q}=\boldsymbol{q}_{n}=\left(\begin{array}{cccc}q_{n}^\theta &q_{n}^\phi \\\end{array}\right)^T $$
If we can estimate the current moment \( \boldsymbol{q} \) from the measured magnetic field \( \boldsymbol{b} \), we can expect to obtain a figure like below.
In this case, we would like to estimate the current moment \( \boldsymbol{q} \) so that the estimated magnetic field \( \boldsymbol{\hat{b}} \) is as close as possible to the measured magnetic field \( \boldsymbol{b} \). Mathematically, this is a typical overdetermined solution called the least squares solution.
In other words, we find \( \boldsymbol{q} \) that minimizes \(\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|\). In this case, it is common to convert it to the square form \(\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2\) for ease of calculation. It is determined that:
$$ \boldsymbol{q}=\underset{\boldsymbol{q}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2=\underset{\boldsymbol{q}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q}\|^2 $$
We introduce the index representing the closeness between the measured value and the estimated value as \(J=\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2=\|\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q}\|^2\). Then,
$$ J=(\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q})^T(\boldsymbol{b}-\boldsymbol{L}\boldsymbol{q})=\boldsymbol{b}^T\boldsymbol{b}-\boldsymbol{b}^T\boldsymbol{Lq}-\boldsymbol{q}^T\boldsymbol{L}^T\boldsymbol{b}+\boldsymbol{q}^T\boldsymbol{L}^T\boldsymbol{L}\boldsymbol{q} $$
When this reaches its minimum value,
$$ \frac{\partial J}{\partial \boldsymbol{q}}=-2\boldsymbol{L}^T\boldsymbol{b}+2(\boldsymbol{L}^T\boldsymbol{L})\boldsymbol{q}=0 $$
That is,
$$ \boldsymbol{q}=\boldsymbol{L}^{-}\boldsymbol{b}=(\boldsymbol{L}^T\boldsymbol{L})^{-1}\boldsymbol{L}^T\boldsymbol{b} $$
And it is solved that:
$$ \boldsymbol{L}^{-}=(\boldsymbol{L}^T\boldsymbol{L})^{-1}\boldsymbol{L}^T $$
In addition, the goodness of fit (GOF) can be considered using the criterion \(J=\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2\) which compares the measured magnetic field \(\boldsymbol{b}\) and the estimated magnetic field \(\boldsymbol{\hat{b}}\) [1].
$$ GOF=1-\frac{\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2}{\|\boldsymbol{b}\|^2} $$
In practice, the estimation involves searching for the location \( \boldsymbol{r} \) that maximizes the GOF over the space in which signals can exist (either the whole brain or a region of interest in the brain). For any position \(\boldsymbol{r}\)
$$ \boldsymbol{q}_{\boldsymbol{r}}=\underset{\boldsymbol{q}_{\boldsymbol{r}}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{L}_{\boldsymbol{r}}\boldsymbol{q}_{\boldsymbol{r}}\|^2=(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b} $$
Hence, \(\boldsymbol{r}\) is determined, and \(\boldsymbol{q}\) is also determined.
$$ \boldsymbol{r}=\underset{\boldsymbol{r}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{L}_{\boldsymbol{r}}(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b}\|^2 $$
$$ \boldsymbol{q}=(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b} $$
This method is called the equivalent current dipole (ECD) estimation or single dipole estimation, and is the gold standard in magnetoencephalography analysis [2]. We will discuss this in the next section.
Summary: The solution of the current moment in n-th lattice point \(\boldsymbol{q}=\boldsymbol{q}_{n}\) for the measured magnetic field \(\boldsymbol{b}\) is an overdetermined system, and using the LFM \(\boldsymbol{L}=\boldsymbol{L}_{n}\), it can be written as \(\boldsymbol{q}=\boldsymbol{L}^{-}\boldsymbol{b}=(\boldsymbol{L}^T\boldsymbol{L})^{-1}\boldsymbol{L}^T\boldsymbol{b}\).
In the next page, we will consider another inverse solution in a situation (underdetermined system or spatial filter) where the number of current dipoles is the same as the number of grid points (N>10,000 for a whole-brain 5 mm voxel) and is overwhelmingly greater than the number of sensors M (=204 or 306).
(References)
- E Kaukoranta, M Hämäläinen, J Sarvas, R Hari: Mixed and sensory nerve stimulations activate different cytoarchitectonic areas in the human primary somatosensory cortex SI. Neuromagnetic recordings and statistical considerations. Exp Brain Res. 1986;63(1):60-6.
- Iida K, Otsubo H, Matsumoto Y, Ochi A, Oishi M, Holowka S, Pang E, Elliott I, Weiss SK, Chuang SH, Snead OC 3rd, Rutka JT. Characterizing magnetic spike sources by using magnetoencephalography-guided neuronavigation in epilepsy surgery in pediatric patients. J Neurosurg. 2005 Mar;102(2 Suppl):187-96.