ABSTRACT: Here, we clarify the principles of magnetoencephalography analysis derived from the Sarvas formula.
In the previous page, we confirmed the Sarvas formula as follows:
Let the center of the virtual sphere be the origin of the position \(\boldsymbol {O}\).Now we consider the magnetic field \(\boldsymbol {b}\) at the position \(\boldsymbol {r}\) when the current dipole of the current moment \(\boldsymbol {q}\) is at the position \(\boldsymbol {r_0}\). Note the magnetic permeability at all positions is equal to the magnetic permeability of the vacuum \(\mu_0\).
The Sarvas formula gives the following analytical solution under this condition.
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi F^2}(F\boldsymbol{q}\times\boldsymbol{r_0}-\boldsymbol{q}\times\boldsymbol{r_0}\cdot\boldsymbol{r}\boldsymbol{\nabla}F) $$
where
$$ \boldsymbol{\nabla}F=(r^{-1}a^2+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r}+2a+2r)\boldsymbol{r}-(a+2r+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r})\boldsymbol{r_0} $$
$$ F=a(ra+r^2-\boldsymbol{r_0}\cdot\boldsymbol{r}),\hspace{10pt}\boldsymbol{a}=\boldsymbol{r}-\boldsymbol{r_0},\hspace{10pt}a=|\boldsymbol{a}|,\hspace{10pt}r=|\boldsymbol{r}| $$
The Sarvas formula gives the following principles:
- Magnetoencephalography analysis requires coordinate of the center of the virtual sphere \(\boldsymbol{O}\).
- Solving the inverse problem in magnetoencephalography analysis is nothing but discussing the current moment \(\boldsymbol{q}\) and the position \(\boldsymbol{r_0}\) of the current dipole .
- The current dipole at the center of the virtual sphere \(\boldsymbol{O}\) does not generate any magnetic field.
- Of the current moments \(\boldsymbol{q}\), the component perpendicular to the center of the virtual sphere \(\boldsymbol{O}\) does not generate any magnetic field (i.e. cannot be discussed in magnetoencephalography analysis).
- The magnetic field \(\boldsymbol{b}(\boldsymbol{r})\) is linear to the current moment of the current dipole \(\boldsymbol{q}\).
- The magnetic field \(\boldsymbol{b}(\boldsymbol{r})\) is non-linear to the position of the current dipole \(\boldsymbol{r_0}\).
Principle 1 is self-evident because the Sarvas equation assumes a spherically symmetric conductor.
Principle 2 is also self-evident because the Sarvas equation assumes a current dipole.
Principles 3 and 4 are also self-evident because \(\boldsymbol{q}\times\boldsymbol{r_0}\) appears in common in the first and second terms of the Sarvas formula. The size of the outer product is the product of the absolute value of the two vectors and the sine angle (the area of the parallelogram formed by the two vectors) as shown in the figure below. Therefore, the size of the cross product gets zero when the current dipole is at the origin \(\boldsymbol{O}\) (i.e. \(\boldsymbol{r_0}\) is a zero vector) or the current moment \(\boldsymbol{q}\) is parallel to the position \(\boldsymbol{r_0}\).
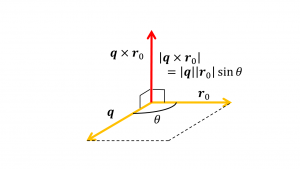
It should be noted that the above discussion does not mean that the brain current has no vertical component, but that it cannot be discussed on the magnetoencephalography. When discussing the vertical components, it is common to consider electroencephalography.
Principle 5 can be proved by examining the definition of linearity for the Sarvas equation. From the Biot-Savart law, which is the basis of the Sarvas formula, the principle of superposition works on the current and the magnetic field, so the magnetic field is constructed as the sum of the magnetic fields generated from multiple current sources (Additiveity). Also, from the first and second terms of the Sarvas formula, the magnetic field \(\boldsymbol{b}\) is proportional to the magnitude of the current moment \(\boldsymbol{q}\) (Homogeneity).
If the position of the current dipole is determined, the linear relationship between the current moment and the magnetic field can be described as a matrix calculation of \(\boldsymbol{b}=\boldsymbol{L}\boldsymbol{q}\). This means that it is easy to solve the inverse problem once the position is fixed. Note, the matrix \(\boldsymbol{L}\) is called as the Lead Field Matrix (LFM).
Furthermore, it can be understood that the estimation of the current dipole is not limited to the single dipole, but also allows multi dipoles of overdetermined system (multi ECD) or underdetermined system (spatial filter).
The non-linearity of principle 6 is self-evident from the complexity of \(\boldsymbol{\nabla}F\) and \(F\).
This characteristic is important in solving the inverse problem. In estimating the current dipole, both the current moment \(\boldsymbol{q}\) and the position \(\boldsymbol{r_0}\) are unknown, and it is necessary to search the signal space due to the non-linearity of the position.
SUMMARY: We confirmed the principle of magnetoencephalography analysis by the Sarvas formula.
In the next page, we will make a preparation for introducing the concept of Lead Field Matrix (LFM). First, we will examine how the Sarvas formula generates magnetic field on the sensors (the sensor array). Then, we will correspond the magnetic field to the output signal of the sensor array.
(Reference)
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.