We introduce the concept of the current dipole and spherically symmetric conductor into the Biot-Savart law to reach the Sarvas formula (Forward solution), which is the analytical solution of the Biot-Savart law.
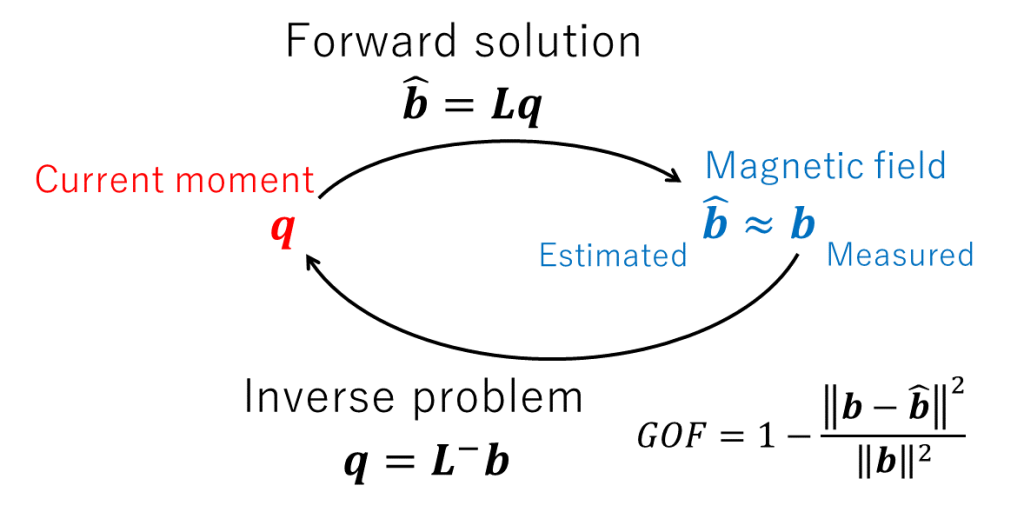
The magnetic field is expressed as \(\boldsymbol{b}\) when outputted by the sensor array, or as \(\boldsymbol{\hat{b}}\) when estimated by the Sarvas equation. Since the estimated magnetic field \(\boldsymbol{\hat{b}}\) from the Sarvas equation is linear to the current moment \(\boldsymbol{q}\), the magnetic field calculation matrix Lead Field Matrix (LFM) is expressed as \(\boldsymbol{L}\) and the linear relationship is written as \(\boldsymbol{\hat{b}}=\boldsymbol{L}\boldsymbol{q}\). Now we are ready to solve the inverse problem to compare the output of the sensor array \(\boldsymbol{b}\) with the estimated \(\boldsymbol{\hat{b}}\).
The relationship between the Forward solution and the Inverse problem is shown in the figure below. Goodness of fit (GOF) is an important concept in overdetermined systems [1].
Let’s start discussing the forward problem in the next page.
(Reference)
- E Kaukoranta, M Hämäläinen, J Sarvas, R Hari: Mixed and sensory nerve stimulations activate different cytoarchitectonic areas in the human primary somatosensory cortex SI. Neuromagnetic recordings and statistical considerations. Exp Brain Res. 1986;63(1):60-6.