Abstract: Here, we confirm the Sarvas formula, which is the basis of magnetoencephalography analysis.
The Sarvas formula is an analytical solution of the Biot-Savart law obtained by introducing the concept of current dipole and assuming a spherically symmetric conductor [1].
The Sarvas formula enables to derive the magnetic field at arbitrary coordinates only by matrix calculation without using integral calculation.
The gist of the Sarvas paper is as follows:
- The Biot-Savart law is transformed using Maxwell’s equations and vector analysis.
- First, uniform and borderless conductor is discussed.
- Next, the concept of equivalent current dipole (ECD) is introduced.
- Then, non-uniform and bounded conductor is discussed.
- Finally, the Sarvas formula is obtained for a spherically symmetric conductor.
The paper uses only three assumptions: Maxwell’s equations, equivalent current dipole, and spherically symmetric conductor. The reason why the center coordinates are required in the magnetoencephalography analysis is that spherically symmetric conductor is assumed.
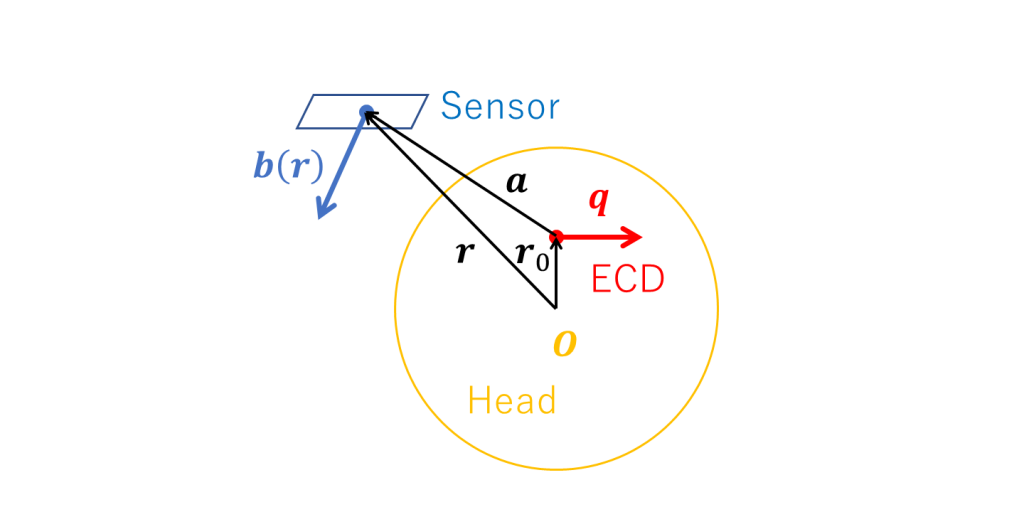
The Sarvas formula is shown below. In the original work, the magnetic field is described as the magnetic field \(\boldsymbol {B}\), but since the magnetic field is a vector, we describe it as \(\boldsymbol {b}\). Similarly, we describe the current moment \(\boldsymbol {Q}\) as \(\boldsymbol {q}\).
Let us consider a spherically symmetric, non-uniform, bounded conductor. Let the center of the virtual sphere be the origin of the position \(\boldsymbol {O}\). Now we consider the magnetic field \(\boldsymbol {b}\) at the position \(\boldsymbol {r}\) when the current dipole of the current moment \(\boldsymbol {q}\) is at the position \(\boldsymbol {r_0}\). Note the magnetic permeability at all positions is equal to the magnetic permeability of the vacuum \(\mu_0\).
Sarvas formula gives the following analytical solution under this condition.
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi F^2}(F\boldsymbol{q}\times\boldsymbol{r_0}-\boldsymbol{q}\times\boldsymbol{r_0}\cdot\boldsymbol{r}\boldsymbol{\nabla}F) $$
where
$$ \boldsymbol{\nabla}F=(r^{-1}a^2+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r}+2a+2r)\boldsymbol{r}-(a+2r+a^{-1}\boldsymbol{a}\cdot\boldsymbol{r})\boldsymbol{r_0} $$
$$ F=a(ra+r^2-\boldsymbol{r_0}\cdot\boldsymbol{r}),\hspace{10pt}\boldsymbol{a}=\boldsymbol{r}-\boldsymbol{r_0},\hspace{10pt}a=|\boldsymbol{a}|,\hspace{10pt}r=|\boldsymbol{r}| $$
The following figure depicts each vector.
Summary: The Sarvas formula is obtained from a few assumptions as an analytical solution of the Biot-Savart law.
In the next page, we confirm the principles of magnetoencephalography analysis using the Sarvas formula.
(Reference)
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.