Abstract: Magnetoencephalography (MEG) begins with the measurement of magnetic fields emitted by the brain. The main source of these fields is believed to be the intracellular current resulting from excitatory postsynaptic potentials (EPSPs) in the dendrites of pyramidal cells in the cerebral cortex.
We discuss the source (current) of the signals (magnetic fields) in magnetoencephalography (MEG).
The source of the magnetic fields measured by MEG is considered to be the intracellular current generated by excitatory postsynaptic potentials (EPSPs) in the dendrites of pyramidal cells distributed in the 5th layer of the cerebral cortex.
Pyramidal cells, the main nerve cells in the cerebral cortex, receive synaptic connections on their dendrites, leading to excitatory postsynaptic potentials that cause the influx of \(Na^+\) and \( Ca^{2+} \) into the cell.
In the cerebral cortex, pyramidal cells extend dendrites vertically to the cortical surface and generate vertical intracellular currents with respect to the cortical surface due to the insulating cell membrane (see the figure below).
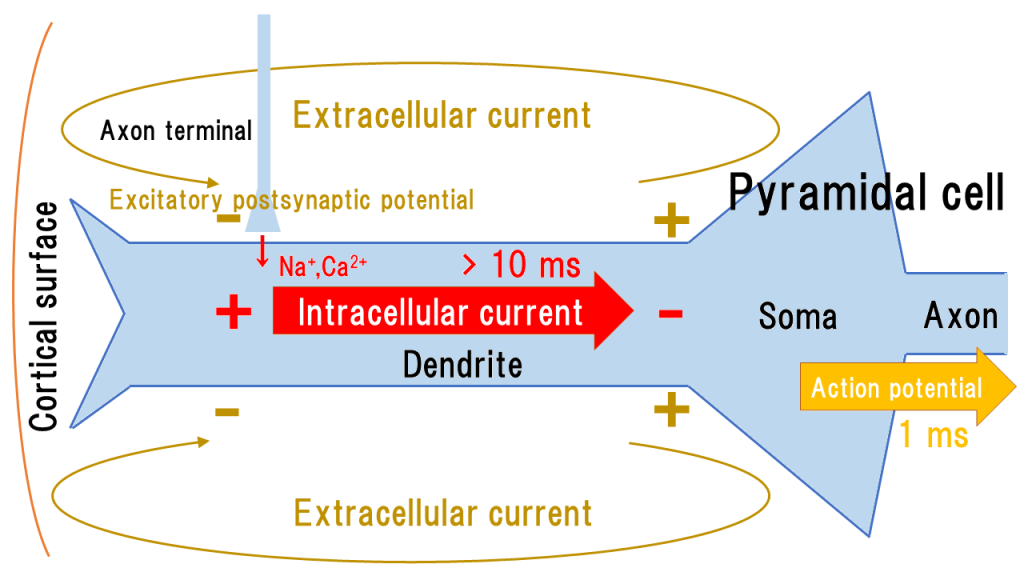
The intracellular current accumulates and becomes the cause of action potentials, which are conducted along the axons.
The intracellular current also generates an extracellular current, which is a volume current.
The length of dendrites is less than 1 mm and only 0.1-0.2 mm contributes to the current moment [1], so the intracellular current in dendrites can be approximated as a point current. Due to the reasons mentioned below, only point currents contribute to the magnetic field.
Since the intracellular current originates from the synaptic junctions, its overall direction depends on the sites where the synapses connect (e.g., fibers from association fibers, commissural fibers, and nonspecific thalamic nuclei are distributed in the 1st layer of the cerebral cortex, while fibers from specific thalamic nuclei are distributed in the 4th layer closer to the soma).
The intracellular current in the dendrites has a duration of several tens of milliseconds, and since many cells can synchronize and superimpose, it is easily captured by MEG.
On the other hand, action potentials that propagate through the axons have a duration of only 1-2 ms, making it difficult for individual cells to synchronize. It is also known that increasing the stimulation intensity does not cause the action potentials to superimpose, but rather increases their frequency (shortens the width of activity). Therefore, action potentials are difficult to capture with MEG (however, there is an expected relationship between action potentials and high-frequency oscillations, which is a topic for future research) [1].
With the intracellular current, an extracellular current is also generated around the dendrites. The extracellular current flows volumetrically, spreading through the extracellular fluid, without being affected by the insulating extracellular membrane. It causes the voltage measured in scalp EEG, but never effects MEG.
In general discussions and textbooks on MEG, to facilitate intuitive understanding and avoid discussions involving equations (such as how currents generate magnetic fields and the cause-effect relationship), the contribution of extracellular current to the magnetic field is often vaguely explained as “extracellular current is symmetrical and does not form a magnetic field outside the sphere” or “extracellular current does not contribute to the magnetic field due to spherical symmetry” [3, 4].
The contribution of intracellular and extracellular currents to the magnetic field is clarified through the consideration of the forward problem by Sarvas [5], which requires knowledge of vector analysis.
We denote the total current density as \( \boldsymbol{j} \), the source current density (intracellular current) as \( \boldsymbol{j}_i \), conductivity as \( \sigma \), electric field as \( \boldsymbol{E} \), and electric potential as \( V \), then the volume current (extracellular current) is given by \( \sigma\boldsymbol{E} \). From Maxwell’s equations,
$$ \boldsymbol{j}=\boldsymbol{j}_i +\sigma\boldsymbol{E}=\boldsymbol{j}_i -\sigma\boldsymbol{\nabla}V $$
When considering a three-dimensional space \( G \), the \( \boldsymbol{j} \) is the total current, so the Biot-Savart law provides the magnetic field \( \boldsymbol{b}(\boldsymbol{r}) \) at position \( \boldsymbol{r} \).
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’ $$
In a region with constant conductivity \( \sigma \), using the Laplacian \( \Delta \), we have
$$ \Delta V=\boldsymbol{\nabla}\cdot\boldsymbol {j}_i / \sigma $$
Thus, using this, we transform \( \boldsymbol{b}(\boldsymbol{r}) \) as follows:
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’ $$
Hence, the magnetic field \( \boldsymbol{b}(\boldsymbol{r}) \) can be expressed solely in terms of the source current density \( \boldsymbol {j}_i \), so the volume current \( \sigma\boldsymbol {E} \) in a spatially homogeneous conductor with uniform conductivity \( \sigma \) does not contribute to the magnetic field \( \boldsymbol{b}(\boldsymbol{r}) \).
Based on this idea, when discussing a spherically symmetric conductor, even if the conductivity is non-uniform, the radial component of the magnetic field \( b_r (\boldsymbol{r}) \) is given by:
$$ b_r (\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}\cdot\boldsymbol {e}_r dv’ $$
Again, the volume current \( \sigma\boldsymbol {E} \) does not contribute to the radial component of the magnetic field \( b_r (\boldsymbol{r}) \).
By approximating this result with a current dipole and integrating, the magnetic field \( \boldsymbol{b}(\boldsymbol{r}) \) is obtained as the Sarvas formula. Ultimately, the volume current \( \sigma\boldsymbol {E} \) does not contribute to the magnetic field \( \boldsymbol{b}(\boldsymbol{r}) \).
From the above, it can be concluded that in magnetoencephalography, only the intracellular current of dendrites, which can be approximated as a point current, contributes to the magnetic field. This conclusion has also been experimentally confirmed [6].
Summary: Pyramidal cells generate intracellular current, action potentials, and extracellular current. Among these, it is believed that the intracellular current in dendrites generates the magnetic field detected by MEG.
In the next page, we will further consider point currents and introduce the concept of current dipoles as a basis for discussing currents in MEG.
(References)
- MS Hämäläinen, R Hari, RJ Ilmoniemi, J Knuutila, OV Lounasmaa: Magnetoencephalography theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993 Apr;65(2):413-97.
- Benavides-Piccione R, Hamzei-Sichani F, Ballesteros-Yáñez I, DeFelipe J, Yuste R. Dendritic size of pyramidal neurons differs among mouse cortical. Cereb Cortex. 2006 Jul;16(7):990-1001.
- Hansen Peter, Morten Kringelbach, and Riitta Salmelin (eds), MEG: An Introduction to Methods. New York, 2010; online edn, Oxford Academic, 1 Sept. 2010.
- Hari Riitta and Puce Aina (eds), MEG-EEG Primer. New York, 2017; online edn, Oxford Academic, 1 Mar. 2017.
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.
- Okada YC, Nicholson C. Magnetic evoked field associated with transcortical currents in turtle cerebellum. Biophys J. 1988 May;53(5):723-31.