Abstract: In order to discuss brain current in magnetoencephalography (MEG), we introduce the concept of current dipole.
In the previous page, we discussed the intracellular currents that serve as the source of the magnetic field generated by the brain in magnetoencephalography (MEG).
However, the brain is structurally complex, even within the cerebral cortex, forming various shapes of brain sulci. The figure below shows the webmaster’s brain (MRI T1WI).
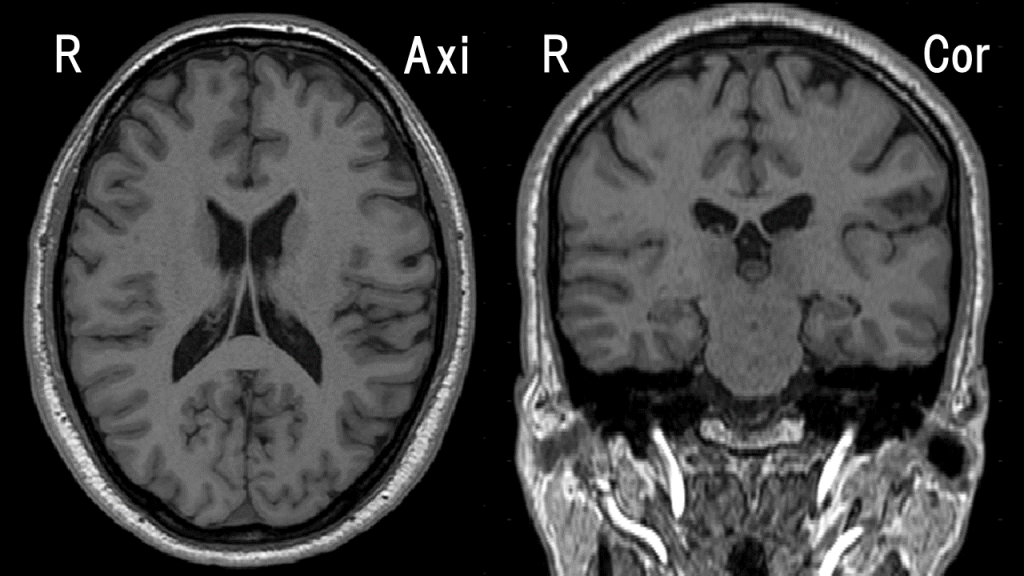
Moreover, the density of pyramidal cells, which are the sources of generation, in the cerebral cortex is very high, reaching 100,000 \( /mm^2\) [1]. The density and thickness of the cortex also vary depending on the location. If the subject has a pathological brain, the complexity and variability increase further. We would like to handle such complex structure and a large number of current sources conveniently.
For this purpose, it would be appropriate to have a summative concept that combines all the small currents in the area of interest. The quantity to be summed should be the current density (unit: \( A/m^2 \)), which is a vector quantity that considers both magnitude and direction, rather than simply the current (unit: \( A \)), which is a scalar quantity and unsuitable for summation.
Additionally, since the volume of interest may vary depending on the situation, it is desirable for this concept itself to have the properties of a point without considering volume. Based on the previous discussion, it can be reasonably argued that giving the characteristics of a point current to this summative concept is justified from the level of microscopic anatomy.
This concept is called an equivalent current dipole (ECD). It has a vector quantity called the current moment, which represents the magnitude and direction of the current, and its unit is
$$ Am (= (A/m^2) \cdot (m^3)) $$
The current dipole has a position, but it is a point and has no volume.
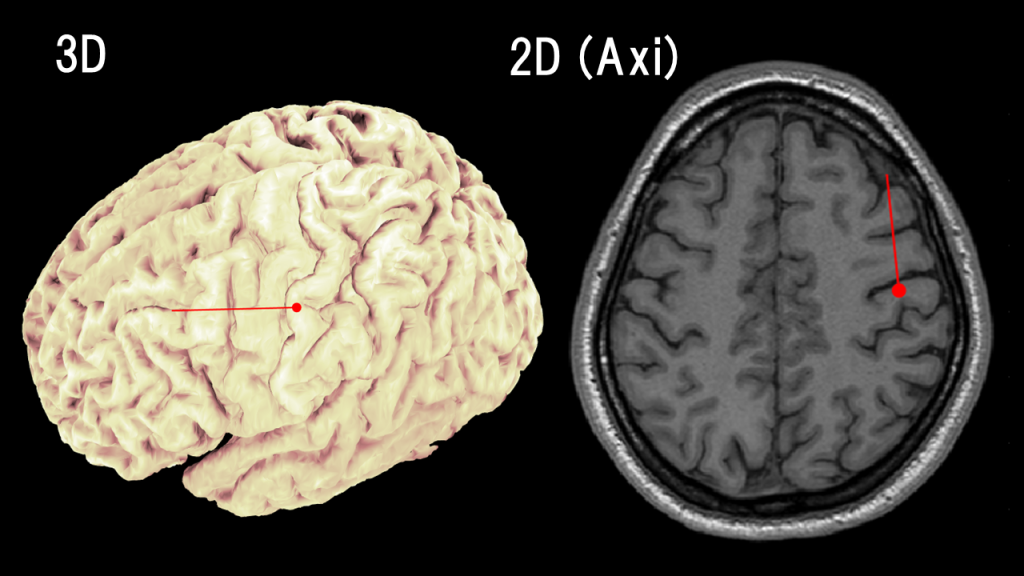
It is customary to superimpose the current dipoles on brain images using matchsticks, where the position is represented by the head of the matchstick, and the direction and magnitude of the current moment are represented by the orientation and size of the needle. The figure below shows an ECD estimation of physiological activity (somatosensory evoked field) in the webmaster’s brain.
The current dipole is defined as a concentration of the current density \( \boldsymbol{j}_i \) at a single point (position \( \boldsymbol{r}_0 \)), and it can be derived mathematically as follows [2]:
The magnetic field \( \boldsymbol{b}(\boldsymbol{r}) \) at position \( \boldsymbol{r} \) caused by the current density \( \boldsymbol {j}(\boldsymbol {r}’) \) in the three-dimensional region \( G \) can be expressed using the Biot-Savart law, under the assumption that the volume current can be neglected as discussed in the previous section:
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’ $$
However, since the volume integration is cumbersome, we want to express it in a more convenient way [2].
First, we can take advantage of the fact that the range of the cortical area targeted by magnetoencephalography measurements is very small, meaning that the three-dimensional region \( G \) is tiny.
Second, we utilize the assumption that the sensors are always located outside the brain, separated by the scalp and the skull. In this case, any position \( \boldsymbol{r}’ \) within \( G \) is sufficiently far away from the sensor position \( \boldsymbol{r} \).
Under the aforementioned assumption, if we represent a small three-dimensional region \( G \) with a position (e.g., the center), we can approximate \( \boldsymbol{r}-\boldsymbol{r}’\simeq\boldsymbol{r}-\boldsymbol{r}_0 \). Hence,
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’\simeq \frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’) dv’\times\frac{\boldsymbol{r}-\boldsymbol{r}_0}{|\boldsymbol{r}-\boldsymbol{r}_0|^3} $$
allows us to move the cross product calculation outside the volume integral. Therefore,
$$ \boldsymbol{q}= \int_G \boldsymbol {j}_i(\boldsymbol {r}’) dv’ $$
defines the electric current moment, and
$$ \boldsymbol{b}(\boldsymbol{r})\simeq \frac{\mu_0}{4\pi}\boldsymbol{q}\times\frac{\boldsymbol{r}-\boldsymbol{r}_0}{|\boldsymbol{r}-\boldsymbol{r}_0|^3} $$
is obtained. By using the Dirac delta function \( \delta (\boldsymbol{r}) \),
$$ \boldsymbol{j}_i (\boldsymbol{r})= \delta (\boldsymbol{r}-\boldsymbol{r}_0) \boldsymbol{q} $$
we can express
$$ \int_G \boldsymbol {j}_i(\boldsymbol {r}’) dv’=\int_G \delta (\boldsymbol{r}’-\boldsymbol{r}_0) \boldsymbol{q} dv’=\boldsymbol{q} $$
In this way, the concept of an electric current dipole avoids complex volume integrals in the derivation of Sarvas formula. Therefore, adopting the concept of electric current dipoles and using Sarvas formula as a solution to the forward problem implies an acceleration of computational processing in magnetoencephalography analysis.
Obviously, the concept of an electric current dipole assumes the representation of current in a small region. Therefore, when discussing current in regions of a certain size, it is necessary to evaluate the validity of the approximation or consider multiple electric current dipoles.
Summary: The concept of an electric current dipole is introduced. Electric current dipoles possess an electric current moment, a vector quantity representing the magnitude and direction of the current, and while they have a position as points, they do not have volume.
In the next page, I would like to discuss the requirement of a minimum unit of electric current moment of 10 nAm in MEG and its rationale.
(References)
- MS Hämäläinen, R Hari, RJ Ilmoniemi, J Knuutila, OV Lounasmaa: Magnetoencephalography theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993 Apr;65(2):413-97.
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.