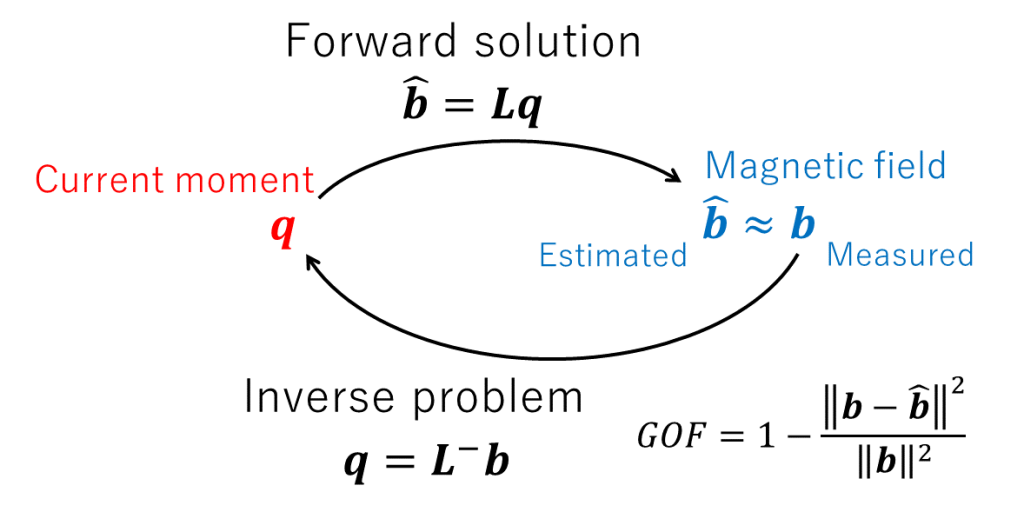
Biot-Savart law に電流双極子の概念を導入して球対称な導体を仮定することで、その解析解である Sarvas 式に至る (Forward solution)。磁場はセンサーアレイの出力 \(\boldsymbol{b}\) という形で表記することにし、Sarvas 式で推定した場合は \(\boldsymbol{\hat{b}}\) と表記することにする。Sarvas式より推定磁場 \(\boldsymbol{\hat{b}}\) は電流モーメント \(\boldsymbol{q}\) に対して線形なので、磁場計算行列 Lead Field Matrix (LFM) を \(\boldsymbol{L}\) とすると、\(\boldsymbol{\hat{b}}=\boldsymbol{L}\boldsymbol{q}\) と表記でき、逆問題 Inverse problem を解く(センサーアレイの出力 \(\boldsymbol{b}\) と 推定出力 \(\boldsymbol{\hat{b}}\) を比較する)準備が完了する。
Forward solution と Inverse problemの関係は下図の通り。あてはまりの良さ goodness of fit (GOF) は Overdetermined system で重要な概念となる [1]。
それでは次項から順問題の議論を始めましょう
(引用)
- E Kaukoranta, M Hämäläinen, J Sarvas, R Hari: Mixed and sensory nerve stimulations activate different cytoarchitectonic areas in the human primary somatosensory cortex SI. Neuromagnetic recordings and statistical considerations. Exp Brain Res. 1986;63(1):60-6.