要旨:磁場をセンサーアレイの出力に対応したベクトルとして表記する。
前項では、脳磁図解析の原則を確認した。
脳磁図解析では多数のセンサー(センサーアレイ)の信号から電流双極子の電流モーメントと位置を推定することになる。
各々のセンサーから出力される信号はスカラーだ。センサーアレイから出力される信号 \( \boldsymbol{s} \) は、センサーの数を M とし、m 番目のセンサーの信号出力を \({s}_{m}\) とすると、
$$ \boldsymbol{s}=\left(\begin{array}{cccc}s_{1} & s_{2} & \ldots & s_{M}\\\end{array}\right)^T $$
とベクトルで表すことができる。管理者が扱っている脳磁計のTRIUX では下図のような正方形のセンサー102組にmagnetometer が1個、planar gradiometer が2個組み込まれているから、M=306 (102 magnetometers + 204 planar gradiometers) だ。
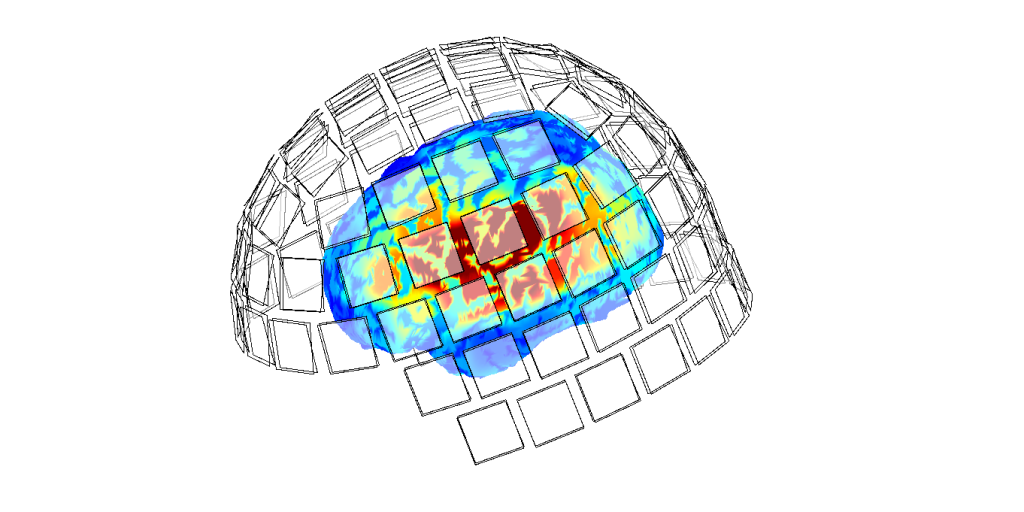
ところでSarvas式の左辺の磁場 \(\boldsymbol{b}(\boldsymbol{r})\) は3次元の方向を持つベクトルだ。それに対してセンサーアレイの信号 \(\boldsymbol{s}\) 成分はスカラーだし、magnetometerかplanar gradiometerかというセンサーの形状による問題もある。
そこでセンサーアレイが電流モーメント \(\boldsymbol{q}\) に対してどう応答するのか調べておく必要がある。
以下では電流双極子の位置 \(\boldsymbol{r}_{0}\) が予め固定されているものとして話を進める。
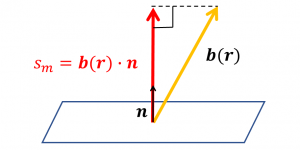
センサーアレイが単純な magnetometer から構成されているなら、下図のように電流モーメント \(\boldsymbol{q}\) と各センサーごとの位置(簡便にはセンサーの中心座標)\(\boldsymbol{r}\) をSarvas式に代入してやり、センサー平面と垂直な成分を取り出してやればよい。計算上はセンサーの単位法線ベクトル \(\boldsymbol{n}\) との内積を求めればよい(脳磁図解析での単位は fT)。
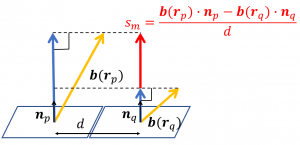
一方で、センサーアレイが planar gradiometer から構成されているなら、下図のように電流モーメント \(\boldsymbol{q}\) と各センサーごとに被差分の位置 \(\boldsymbol{r}_{p}\)、差分の位置 \(\boldsymbol{r}_{q}\) をSarvas 式に代入してやり、それぞれセンサーの単位法線ベクトル \(\boldsymbol{n}_{p}\), \(\boldsymbol{n}_{q}\) との内積を求め、差を求めて、最後に被差分中心・差分中心間の距離で割ればよい(脳磁図解析での単位は fT/cm)。
こうして3次元ベクトルとしての磁場 \(\boldsymbol{b}(\boldsymbol{r})\) をセンサーアレイの出力 \(\boldsymbol{s}\) に対応させることができた。
以後は磁場 \(\boldsymbol{b}\) といったら M 次元列ベクトルのセンサーアレイ出力(上記の議論の \(\boldsymbol{s}\))だと考えよう。すなわち、センサーアレイから出力される信号 \( \boldsymbol{b} \) は、センサーの数を M とし、m 番目のセンサーの信号出力を \(b_{m}\) とすると、
$$ \boldsymbol{b}=\left(\begin{array}{cccc}b_{1} & b_{2} & \ldots & b_{M}\\\end{array}\right)^T $$
まとめ:磁場をセンサーアレイの出力に対応したセンサー数次元のベクトルとして表記できた。
次項では、電流モーメントに対する磁場の線形性を利用して \(\boldsymbol{b}=\boldsymbol{L}\boldsymbol{q}\) と表記したときの \(\boldsymbol{L}\) を求めることを考える。これは磁場計算行列 Lead Feld Matrix (LFM) と呼ばれるもので、逆問題を高速に処理するためには必要不可欠な概念だ。