要旨:LFM を構成することで逆問題を解く準備が完了する。
前項では、Lead field matrix (LFM) を導入する前に Sensor array について述べた。
Sarvas式により順問題は解けた。すなわち、電流双極子の電流モーメントと位置が分かれば任意の位置における磁場(センサーの信号)が分かる。
ところで実際に測定したセンサーアレイの出力信号 \( \boldsymbol{b} \) と Sarvas 式を用いて推定した理論的な出力信号 \(\boldsymbol{\hat{b}} \) は様々な要因で異なる。以下、両者を区別することにしよう。
前項での考察から、センサーアレイから出力される信号を Sarvas 式を用いて推定した \( \boldsymbol{\hat{b}} \) は、センサーの数を M とし、m 番目のセンサーの推定信号出力を \(\hat{b}_{m} \) とすると、
$$ \boldsymbol{\hat{b}}=\left(\begin{array}{cccc}\hat{b}_{1} & \hat{b}_{2} & \ldots & \hat{b}_{M} \\\end{array}\right)^T $$
と表される。
電流モーメントに対する磁場の線形性から、推定磁場と電流モーメントは行列で表現できる。そこで \(\boldsymbol{\hat{b}}=\boldsymbol{L}\boldsymbol{q}\) と表記したときの \(\boldsymbol{L}\) を求めることを考える。
Sarvas式が示す原則から、センサーの信号は電流モーメントに対しては線形だけれども、位置に対しては非線形で空間の探索を要するのであった。
そこで、任意の位置における単位電流モーメントに対する各センサーの信号を予め調べておく方法が考えられる。これは一般的にはアレイ応答ベクトルなどと呼ばれるが、脳磁図解析においては Lead field という呼び方が一般的だ [1]。各次元に対するアレイ応答ベクトルを磁場計算ベクトル Lead field vector、各次元をまとめて磁場計算行列 Lead field matrix (LFM) と呼ぶ。
いま、M個のセンサーで脳をN個の格子点に分割することを考えたい(5mm幅で格子点を作成するなら、下図のごとく管理者の大脳でN=14,000個の格子点に分割される)。
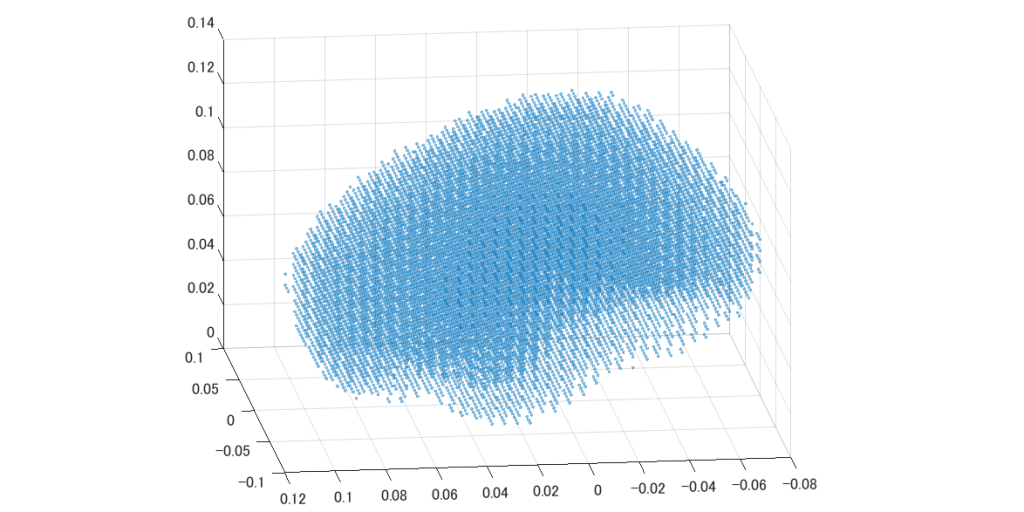
格子点がN個あるとき、n番目の格子点におけるLFMを \(\boldsymbol{L}_{n}\) とする。直交座標で考え、xyzの各成分となる列ベクトル(アレイ応答ベクトル)をそれぞれ \(\boldsymbol{l}_{n} ^x\), \(\boldsymbol{l}_{n} ^y\), \(\boldsymbol{l}_{n} ^z\) とする。さらに x 軸方向の単位電流モーメントに対する m 番目のセンサーにおける磁場のスカラー値を \(l_{n_m}^x\) などと書き、格子点の n 番目にある電流双極子の電流モーメントを \(\boldsymbol{q}_{n}\) とすると、
$$ \boldsymbol{L}_{n}=\left(\begin{array}{cccc}\boldsymbol{l}_{n}^x &\boldsymbol{l}_{n}^y & \boldsymbol{l}_{n}^z\\\end{array}\right)=\left(\begin{array}{cccc}l_{n_1}^x & l_{n_1}^y & l_{n_1}^z \\l_{n_2}^x & l_{n_2}^y & l_{n_2}^z \\\vdots & \vdots & \vdots \\l_{n_M}^x & l_{n_M}^y & l_{n_M}^z \\\end{array}\right) $$
$$ \boldsymbol{q}_{n}=\left(\begin{array}{cccc}q_{n}^x &q_{n}^y & q_{n}^z\\\end{array}\right)^T $$
となる。各センサーの推定値は
$$ \boldsymbol{\hat{b}}=\boldsymbol{L}_{n}\boldsymbol{q}_{n} $$
と簡便な形で求まり、LFM を構成した効果が出ている。
ところで、このまま実際のセンサーの値 \(\boldsymbol{b}\) と推定値 \(\boldsymbol{\hat{b}}\) を比較することで逆問題を解いても問題なさそうだが、Sarvas式より、電流双極子の電流モーメントのうち、仮想球中心に対して垂直な成分は磁場を発生しないのであった。つまり、せっかく逆問題を解いて \(\boldsymbol{q}_{n}\) を推定しても垂直成分は議論できないので除去する必要が生じる。
それなら初めから直交座標ではなく、極座標で議論してやればよい。
$$ \boldsymbol{L}_{n}=\left(\begin{array}{cccc}\boldsymbol{l}_{n}^\theta &\boldsymbol{l}_{n}^\phi & \boldsymbol{l}_{n}^r \\\end{array}\right) $$
$$ \boldsymbol{q}_{n}=\left(\begin{array}{cccc}q_{n}^\theta &q_{n}^\phi & q_{n}^r\\\end{array}\right)^T $$
となるが、\(\boldsymbol{l}_{n}^r\) は全ての成分がゼロのゼロベクトルだし、\(q_{n}^r\) は議論できないので、結局
$$ \boldsymbol{L}_{n}=\left(\begin{array}{cccc}\boldsymbol{l}_{n}^\theta &\boldsymbol{l}_{n}^\phi \\\end{array}\right) $$
$$ \boldsymbol{q}_{n}=\left(\begin{array}{cccc}q_{n}^\theta &q_{n}^\phi \\\end{array}\right)^T $$
と、次元を一つ落とすことができる。以下はこの考えに沿ってLFMを考えよう。
格子点を複数個選んでLFMを構成することもできる。例えばa番目とb番目の格子点を選んでLFMを構成する場合、
$$ \boldsymbol{L}_{ab}=\left(\begin{array}{cccc}\boldsymbol{l}_{a}^\theta &\boldsymbol{l}_{a}^\phi & \boldsymbol{l}_{b}^\theta&\boldsymbol{l}_{b}^\phi \\\end{array}\right) $$
$$ \boldsymbol{q}_{ab}=\left(\begin{array}{cccc}q_{a}^\theta &q_{a}^\phi & q_{b}^\theta &q_{b}^\phi \\\end{array}\right)^T $$
となり、各センサーの推定値は
$$ \boldsymbol{\hat{b}}=\boldsymbol{L}_{ab}\boldsymbol{q}_{ab} $$
とはいえ、Multi ECD 推定では、格子点を選ぶ組み合わせを考えなければならないので、直接推定するのは大変だ(格子点14,000個から2つ選ぶなら約1億通り、3つ選ぶなら約4600億通り)。MUSICアルゴリズムを使用するなどの技法が必要になってくる。
全格子点でLFMを構成することも可能で、こちらは空間フィルターの基本的な考え方だ。全格子点を選んでいるので、組み合わせを考える必要はない(全て選ぶ組み合わせは 1 通り)。
$$ \boldsymbol{L}_{all}=\left(\begin{array}{cccc}\boldsymbol{l}_{1}^\theta &\boldsymbol{l}_{1}^\phi & \ldots & \ldots & \boldsymbol{l}_{N}^\theta &\boldsymbol{l}_{N}^\phi \\\end{array}\right) $$
$$ \boldsymbol{q}_{all}=\left(\begin{array}{cccc}q_{1}^\theta & q_{1}^\phi & \ldots & \ldots & q_{N}^\theta & q_{N}^\phi \\\end{array}\right)^T $$
となり、各センサーの推定値は
$$ \boldsymbol{\hat{b}}=\boldsymbol{L}_{all}\boldsymbol{q}_{all} $$
となる。
これで逆問題を解く用意はできた。
まとめ:LFM を構成することで逆問題を解く用意ができた。
次節では、実際のセンサーの値 \(\boldsymbol{b}\) と推定値 \( \boldsymbol{\hat{b}} \) を比較することで逆問題を解いていきたい。
(引用)
- MS Hämäläinen, RJ Ilmoniemi: Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput. 1994 Jan;32(1):35-42.