要旨:劣決定系の逆問題の数学的解である MNE は解析の実情に合わず、空間フィルターが発展する動機となった。
前項では、劣決定解である空間フィルター Spatial Filter の呼称について言及した。
ここでは、空間フィルターのうち、Minimum Norm Estimate (MNE) を通じて、Non-adaptive Beamformer についての議論を始めたい。解は劣決定解だし、Non-adaptive なので対象とする情報は 1 サンプル(ある瞬間のセンサーアレイが出力する信号 \(\boldsymbol{b}\))だ。
電流双極子の位置が定まった状態で、電流モーメント \(\boldsymbol{q}\) と磁場 \(\boldsymbol{b}\) の間に成立する線形写像、Lead Field Matrix (LFM) を \( \boldsymbol{L} \) とすると、
$$ \boldsymbol{b}=\boldsymbol{L}\boldsymbol{q} $$
であり、磁場から電流モーメントを推定する
$$ \boldsymbol{q}=\boldsymbol{L}^-\boldsymbol{b} $$
の逆の対応関係(逆線形写像) \(\boldsymbol{L}^{-}\) を求めたい。
空間フィルターは信号空間の全てから信号が出ていると仮定するのが基本で、\(\boldsymbol{q}=\boldsymbol{q}_{all}\), \(\boldsymbol{L}=\boldsymbol{L}_{all}\) だ。
$$ \boldsymbol{b}=\boldsymbol{L}\boldsymbol{q} $$
の数学的な解は劣決定解なので、
$$ \boldsymbol{q}=\boldsymbol{L}^{-}\boldsymbol{b}=\boldsymbol{L}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
で、導出過程に由来してミニマムノルム推定Minimum Norm Estimate (MNE) と呼ばれる [1]。
MNE は、その導出過程で信号全体をできるだけ小さくするよう要請しており、センサーの信号をセンサーに近い格子点だけで説明するような解が得られる。つまり、センサーに近い格子点の信号が相対的に強くなってしまう [2]。脳磁図であれば下図のように脳表に散在した信号が解析結果として得られる。
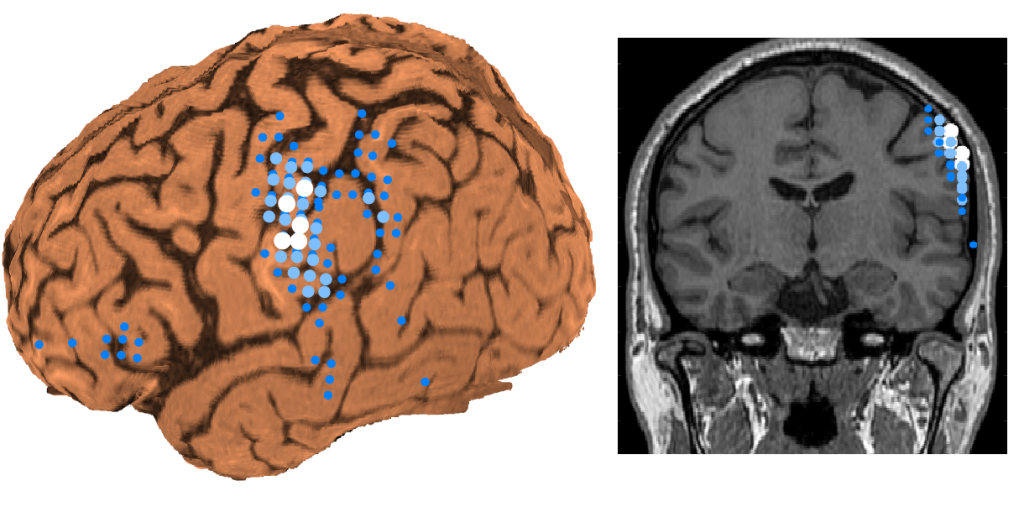
これはこれで良いのだが、実際の脳磁図解析では、てんかん活動の推定など、Single-dipole estimation のように信号源をある程度の深さにある 1 か所の焦点として想定したい場合も多い。つまり、MNE は脳磁図解析の実情に合わないことが多い。
MNE が実情に合わない原因は、電流モーメントの大きさが電流双極子の位置(所属する格子点の位置)に依存していることが原因だ。
$$ \boldsymbol{q}=\boldsymbol{L}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
を書き直して、
$$ \left(\begin{array}{cccc}\boldsymbol{q}_{1} \\ \vdots \\ \boldsymbol{q}_{N}\end{array}\right)=\left(\begin{array}{cccc}\boldsymbol{L}_{1}^{T} \\ \vdots \\ \boldsymbol{L}_{N}^{T}\end{array}\right) (\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
ただし、信号空間(典型的には全脳)の格子点数は N で、
$$ \boldsymbol{q}_{n}=\left(\begin{array}{cccc}q_{n}^{\theta} & q_{n}^{\phi} \end{array} \right)^{T} $$
$$ \boldsymbol{q}=\boldsymbol{q}_{all}=\left(\begin{array}{cccc}q_{1}^{\theta} & q_{1}^{\phi} & \ldots & \ldots & q_{N}^{\theta} & q_{N}^{\phi} \end{array} \right)^{T} $$
$$ \boldsymbol{L}_{n}=\left(\begin{array}{cccc}\boldsymbol{l}_{n}^{\theta} & \boldsymbol{l}_{n}^{\phi} \end{array} \right)= \left(\begin{array}{cccc} l_{n_1}^{\theta} & l_{n_1}^{\phi} \\ \vdots & \vdots \\ l_{n_M}^{\theta} & l_{n_M}^{\phi} \end{array} \right) $$
$$ \boldsymbol{L}=\boldsymbol{L}_{all}=\left(\begin{array}{cccc}\boldsymbol{L}_{1} & \ldots & \boldsymbol{L}_{N} \end{array} \right)= \left(\begin{array}{cccc}\boldsymbol{l}_{1}^{\theta} & \boldsymbol{l}_{1}^{\phi} & \ldots & \ldots & \boldsymbol{l}_{N}^{\theta} &\boldsymbol{l}_{N}^{\phi} \end{array} \right) $$
とすれば、
$$ \boldsymbol{q}_{n}=\boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
であり、フロベニウスノルム Frobenius norm を用いて、ノルムの劣乗法性から
$$ \|\boldsymbol{q}_{n}\|=\| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} \| \leq \| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F} \| \boldsymbol{b} \| $$
となり、
$$ \frac{\|\boldsymbol{q}_{n}\|}{\|\boldsymbol{b} \|} \leq \| \boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\|_{F} $$
となって、電流モーメントの(測定磁場の大きさに対する相対的な)大きさの最大値が格子点ごとに LFM に依存していることがわかる。これがMNEの解の分布を規定している。
この最大値の呪縛から脱却するためには、新たな評価基準を作る必要がある。例えば電流モーメントをこの大きさで割って標準化するなどして新たな評価基準をつくれば良い。この手法はDynamic statistical parametric mapping (dSPM)とかWeight (noise) normalized minimum norm filterなどと呼ばれる[3]。
一般化した新たな評価基準を、n 番目の格子点について \(\boldsymbol{q}_{n_{filtered}}\) と書き、線形逆写像 \( \boldsymbol{L}_{n}^{-} \) に対応した重み行列を \(\boldsymbol{W}_{n}^{T}\) とすると、
$$ \boldsymbol{q}_{n_{MNE}}= \boldsymbol{q}_{n}=\boldsymbol{L}_{n}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
$$ \boldsymbol{q}_{n_{filtered}}= \boldsymbol{W}_{n}^T\boldsymbol{b} $$
$$ \boldsymbol{W}_{n}=\left(\begin{array}{cccc} \boldsymbol{w}_{n}^{\theta} & \boldsymbol{w}_{n}^{\phi} \end{array} \right)= \left(\begin{array}{cccc} w_{n_1}^{\theta} & w_{n_1}^{\phi} \\ \vdots & \vdots \\ w_{n_M}^{\theta} & w_{n_M}^{\phi} \end{array} \right) $$
となり、
$$ \boldsymbol{q}_{MNE}= \boldsymbol{q}=\boldsymbol{L}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1}\boldsymbol{b} $$
$$ \boldsymbol{q}_{filtered}= \boldsymbol{W}^T\boldsymbol{b} $$
$$ \boldsymbol{W}^{T}= \left(\begin{array}{cccc} \boldsymbol{W}_{1}^{T} \\ \vdots \\ \boldsymbol{W}_{M}^{T} \end{array} \right) $$
と書ける。MNEについてはもちろん
$$ \boldsymbol{W}^{T}=\boldsymbol{W}_{MNE}^{T}= \left(\begin{array}{cccc} \boldsymbol{L}_{1}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1} \\ \vdots \\ \boldsymbol{L}_{N}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1} \end{array} \right) =\boldsymbol{L}^T(\boldsymbol{L}\boldsymbol{L}^{T})^{-1} $$
だ。
ところで、逆問題を解くことは、逆線形写像 \( \boldsymbol{L}^{-} \) を求めて電流モーメント \(\boldsymbol{q}\) を定めることであったはずだ。すなわち、以下の解を求めることであったはずだ。
$$ \boldsymbol{q}=\boldsymbol{L}^{-}\boldsymbol{b} $$
しかし、空間フィルターを構成すること(重み行列 \(\boldsymbol{W}^{T}\) を求めて評価基準値 \(\boldsymbol{q}_{filtered}\) を定めること)に話がすり替わった。すなわち、以下の解を求めることに話がすり替わった。
$$ \boldsymbol{q}_{filtered}= \boldsymbol{W}^T\boldsymbol{b} $$
逆問題を解くという概念が空間フィルターの構成に拡張され、電流モーメント \(\boldsymbol{q}\) を定めることから評価基準値 \(\boldsymbol{q}_{filtered}\) を定めることに拡張されたと解釈することもできる。
評価基準値 \(\boldsymbol{q}_{filtered}\) は仮想値であり、重み行列 \(\boldsymbol{W}^{T}\) を工夫することで柔軟に提案することができる。空間フィルターを構成することは、目的に応じた評価基準値 \(\boldsymbol{q}_{filtered}\) を提案するために、重み行列 \(\boldsymbol{W}^{T}\) を提案することに他ならない(下図)。
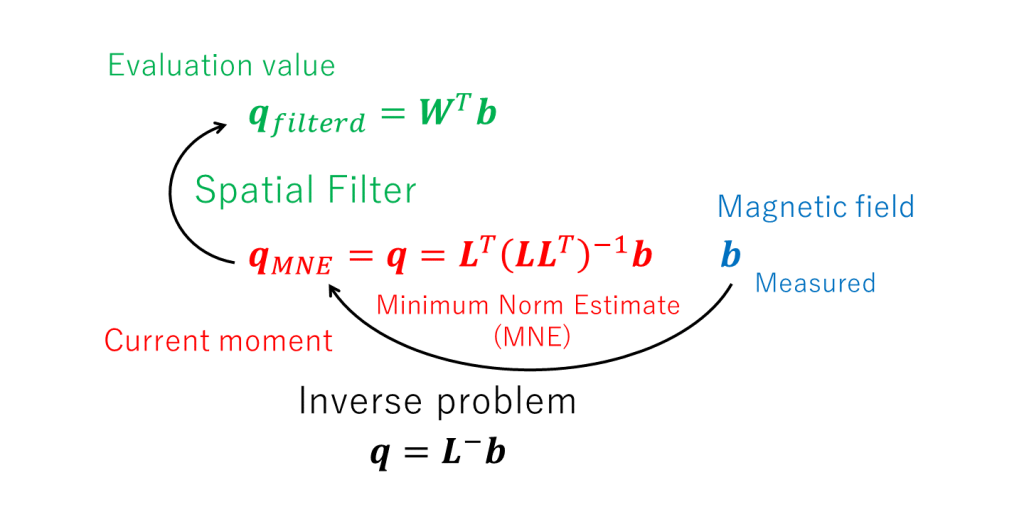
まとめ:劣決定解の逆問題を解くという概念は、空間フィルターを構成することに拡張された。
次項では代表的なNon-adaptive beam former であるdSPM, sLORETA, SMF について議論したい。
(引用)
- MS Hämäläinen, RJ Ilmoniemi: Interpreting magnetic fields of the brain: minimum norm estimates. Med Biol Eng Comput. 1994 Jan;32(1):35-42.
- Kensuke Sekihara, Maneesh Sahani, Srikantan S Nagarajan: Localization bias and spatial resolution of adaptive and non-adaptive spatial filters for MEG source reconstruction. Neuroimage. 2005 May 1;25(4):1056-67.
- AM Dale, AK Liu, BR Fischl, RL Buckner, JW Belliveau, JD Lewine, E Halgren: Dynamic statistical parametric mapping: combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron. 2000 Apr;26(1):55-67.