要旨:ECD 推定の妥当性について、代表的な指標に、当てはまりの良さ goodness of fit (GOF) と信頼体積 confidence volume (CV) がある。
前項では、脳磁図 magnetoencephalography (MEG) の解として、等価電流双極子 equivalent current dipole (ECD) 推定という優決定解を得た。すなわち、dipole の位置を \(\boldsymbol{r}\)、その位置における単位電流源に対するセンサー応答行列 lead field matrix (LFM) を \(\boldsymbol{L}_{\boldsymbol{r}}\)、dipole の電流モーメントを \(\boldsymbol{q}\)、任意の時刻における測定磁場を \(\boldsymbol{b}\) とすると
$$ \boldsymbol{r}=\underset{\boldsymbol{r}}{\arg\min}\|\boldsymbol{b}-\boldsymbol{L}_{\boldsymbol{r}}(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b}\|^2 $$
$$ \boldsymbol{q}=(\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{L}_{\boldsymbol{r}})^{-1}\boldsymbol{L}_{\boldsymbol{r}}^T\boldsymbol{b} $$
さらに、ECD 推定の妥当性について代表的な指標に当てはまりの良さ goodness of fit (GOF) が知られていることを述べた。推定磁場 \(\boldsymbol{\hat{b}}=\boldsymbol{L_{\boldsymbol{r}} \boldsymbol{q}}\) に対して
$$ GOF=1-\frac{\|\boldsymbol{b}-\boldsymbol{\hat{b}}\|^2}{\|\boldsymbol{b}\|^2}=1-\frac{\|\boldsymbol{b}-\boldsymbol{L_{\boldsymbol{r}}}\boldsymbol{q}\|^2}{\|\boldsymbol{b}\|^2} $$
ほかにも信頼体積 confidence volume (CV) という指標も知られている [1]。これは信号が背景ノイズからどの程度突出しているか、信号雑音比 signal-to-noise ratio (SNR) を考慮して、ECD が 95% 以上の確率で存在する空間を楕円体の体積で表した指標だ。GOF が 線形な求解の産物だとすると、CV は非線形な求解の産物と言える。そのため、CV の理解には最尤推定 maximum likelihood estimation という数理統計学的な考え方が必要になる[2,3]。
1. 背景活動の設定
まず、信号源(電流源)が、正規分布する有限の未知パラーメータ \( \boldsymbol{\beta} \) で記述できるとする。脳磁図において信号源のパラメータ数は 5 だ \((k = 5)\)
$$ \boldsymbol{\beta}=\left(\begin{array}{cccc}\beta_{1} & \beta_{2} & \ldots & \beta_{k} \\\end{array}\right)^{T} $$
$$ =\left(\begin{array}{cccc}r_{x} & r_{y} & r_{z} & q_{\theta} & q_{\phi} \\\end{array}\right)^{T} $$
センサー \(P_{i} (i=1,2,…,m)\) における測定磁場を \(b_{i}\) とし、推定磁場を \(\hat{b}_{i}(\boldsymbol{\beta})\) とすると
$$ \boldsymbol{\hat{b}}(\boldsymbol{\beta})=\left(\begin{array}{cccc}\hat{b}_{1}(\boldsymbol{\beta}) & \hat{b}_{2}(\boldsymbol{\beta}) & \ldots & \hat{b}_{m}(\boldsymbol{\beta}) \\\end{array}\right)^{T} $$
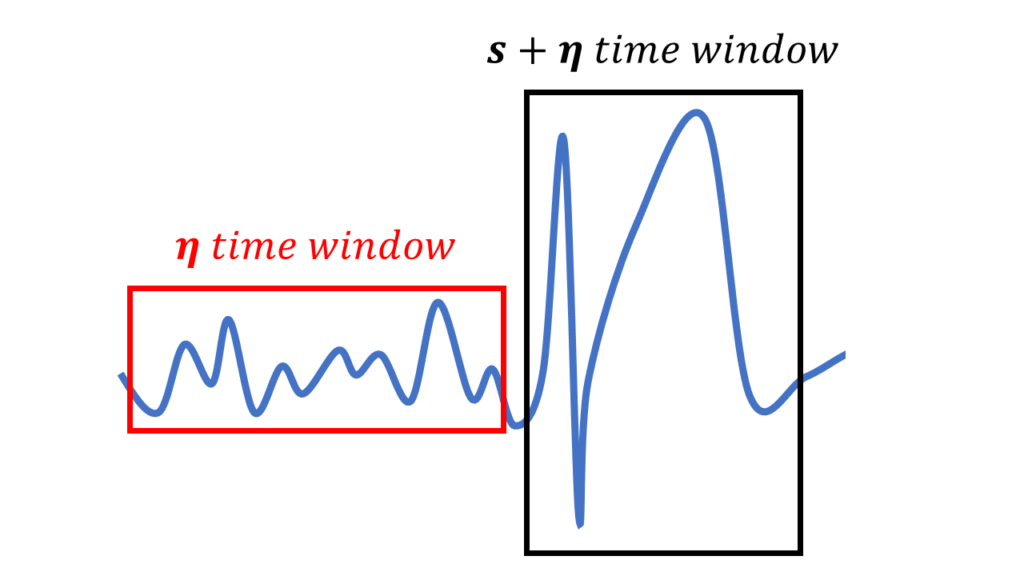
測定磁場 \(\boldsymbol{b}\) は信号 \(\boldsymbol{s}\) とノイズ \(\boldsymbol{\eta}\) で構成されているとする
$$ \boldsymbol{b}=\boldsymbol{s}+\boldsymbol{\eta} $$
ノイズ \(\boldsymbol{\eta}\) の共分散行列 \(\boldsymbol{\Sigma}\) は
$$ \boldsymbol{\Sigma}=\boldsymbol{E}[ \boldsymbol{\eta}\boldsymbol{\eta}^T ] $$
実際の脳磁図測定において、ノイズは \(\boldsymbol{\eta}\) のようにある一時点では評価せず、ある程度時間幅があって安定した低振幅の背景活動を選び、時間幅のあるノイズ \(\boldsymbol{H}\) で評価することが多い。
$$ \boldsymbol{H}=\left(\begin{array}{cccc}\boldsymbol{\eta}_{\ t=t_{1}} & \boldsymbol{\eta}_{\ t=t_{2}} & \ldots & \boldsymbol{\eta}_{\ t=t_{n}} \\\end{array}\right) $$
この場合も
$$ \boldsymbol{\Sigma}=\boldsymbol{E}[ \boldsymbol{H}\boldsymbol{H}^T ] $$
となって共分散行列 \(\boldsymbol{\Sigma}\) は時間幅に関わらず \(m\) 次正方行列であることに変わりはない。
2. 最尤推定
多変量正規分布の確率密度関数は次のようになることを思い出し、
$$ f(\boldsymbol{x}; \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{(2\pi)^{p/2}(det \boldsymbol{\Sigma})^{1/2}} exp(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})) $$
尤度(観測値 \( x_{1},x_{2},…,x_{N} \) に対する確率密度関数の総積 \(p(x_{1})p(x_{2})…p(x_{N})\) を最大にするように未知パラメータの値を推定する最尤推定の立場から、上式は次のように指数の項の正負を逆にしたものを最小化する式に書き直される
$$ S(\boldsymbol{\beta})=(\hat{\boldsymbol{b}}(\boldsymbol{\beta})-\boldsymbol{b})^{T}\boldsymbol{\Sigma}^{-1}(\hat{\boldsymbol{b}}(\boldsymbol{\beta})-\boldsymbol{b}) $$
言い換えると、統計学的な距離(マハラノビス距離 Mahalanobis distance の二乗)を最小化することに他ならない
以下では、推定磁場 \(\hat{\boldsymbol{b}}(\boldsymbol{\beta})\) はノイズが無いから解 \(\boldsymbol{\hat{\beta}}\) に対して
$$ \boldsymbol{\hat{b}}(\boldsymbol{\hat{\beta}})=\boldsymbol{s} $$
と考えて議論を進める
3. 線形近似と信頼体積
解 \(\boldsymbol{\hat{\beta}}\) から推定されるパラメータを \(\boldsymbol{\gamma}\) として解の信頼性を評価する。 \(\boldsymbol{\gamma}\) は \(\boldsymbol{\hat{\beta}}\) の近傍にあり、線形近似できるものとする。
\(\boldsymbol{\hat{\beta}}\) における \(\boldsymbol{\hat{b}}\) のヤコビ行列を \(\boldsymbol{A}\) とすると
$$ A_{ij}=\left.\frac{\partial\hat{b}_{i}}{\partial\beta_{j}}\right|_{\boldsymbol{\beta}=\boldsymbol{\hat{\beta}}} (i=1,2,…,m; j=1,2,…,k) $$
すなわち
$$ \boldsymbol{A}=\left(\begin{array}{cccc}\left.\frac{\partial\boldsymbol{\hat{b}}(\boldsymbol{\beta})}{\partial r_{x}}\right|_{\boldsymbol{\beta}=\boldsymbol{\hat{\beta}}} & \left.\frac{\partial\boldsymbol{\hat{b}}(\boldsymbol{\beta})}{\partial r_{y}}\right|_{\boldsymbol{\beta}=\boldsymbol{\hat{\beta}}} & \left.\frac{\partial\boldsymbol{\hat{b}}(\boldsymbol{\beta})}{\partial r_{z}}\right|_{\boldsymbol{\beta}=\boldsymbol{\hat{\beta}}} &\left.\frac{\partial\boldsymbol{\hat{b}}(\boldsymbol{\beta})}{\partial q_{\theta}}\right|_{\boldsymbol{\beta}=\boldsymbol{\hat{\beta}}} & \left.\frac{\partial\boldsymbol{\hat{b}}(\boldsymbol{\beta})}{\partial q_{\phi}}\right|_{\boldsymbol{\beta}=\boldsymbol{\hat{\beta}}} \\\end{array}\right) $$
線形近似は
$$ \boldsymbol{\hat{b}}(\boldsymbol{\beta})\approx\boldsymbol{\hat{b}}(\boldsymbol{\gamma})+\boldsymbol{A}(\boldsymbol{\beta}-\boldsymbol{\gamma}) $$
最尤推定は
$$ S(\boldsymbol{\beta})=(\hat{\boldsymbol{b}}(\boldsymbol{\beta})-\boldsymbol{b})^{T}\boldsymbol{\Sigma}^{-1}(\hat{\boldsymbol{b}}(\boldsymbol{\beta})-\boldsymbol{b}) $$
$$ =(\boldsymbol{\hat{b}}(\boldsymbol{\gamma})+\boldsymbol{A}(\boldsymbol{\beta}-\boldsymbol{\gamma})-\boldsymbol{b})^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{\hat{b}}(\boldsymbol{\gamma})+\boldsymbol{A}(\boldsymbol{\beta}-\boldsymbol{\gamma})-\boldsymbol{b}) $$
$$ =\boldsymbol{\hat{b}}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{\hat{b}}+\boldsymbol{\hat{b}}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\beta}-\boldsymbol{\hat{b}}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\gamma}-\boldsymbol{\hat{b}}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{b} $$
$$ +\boldsymbol{\beta}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{\hat{b}}+\boldsymbol{\beta}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\beta}-\boldsymbol{\beta}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\gamma}-\boldsymbol{\beta}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{b} $$
$$ -\boldsymbol{\gamma}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{\hat{b}}-\boldsymbol{\gamma}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\beta}+\boldsymbol{\gamma}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\gamma}+\boldsymbol{\gamma}^{T}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{b} $$
$$ -\boldsymbol{b}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{\hat{b}}-\boldsymbol{b}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\beta}+\boldsymbol{b}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\gamma}+\boldsymbol{b}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{b} $$
\(S(\boldsymbol{\beta})\) が最小化するとき
$$ \frac{\partial S(\boldsymbol{\beta})}{\partial\boldsymbol{\beta}}=2\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{\hat{b}}+2\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\beta}-2\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{b}-2\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A\gamma}=0 $$
$$ \boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A}(\boldsymbol{\beta}-\boldsymbol{\gamma})-\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{b}-\boldsymbol{\hat{b}})=0 $$
$$ \boldsymbol{\hat{\beta}}=\boldsymbol{\gamma}+(\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}(\boldsymbol{b}-\boldsymbol{\hat{b}}(\boldsymbol{\gamma})) $$
\(\boldsymbol{b}-\hat{\boldsymbol{b}}(\boldsymbol{\gamma})\approx\boldsymbol{b}-\boldsymbol{s}=\boldsymbol{\eta}\) だから
$$ \boldsymbol{E}[(\boldsymbol{\hat{\beta}}-\boldsymbol{\gamma})(\boldsymbol{\hat{\beta}}-\boldsymbol{\gamma})^{T}]=\boldsymbol{E}[(\boldsymbol{\gamma}-\boldsymbol{\hat{\beta}})(\boldsymbol{\gamma}-\boldsymbol{\hat{\beta}})^{T}] $$
$$ =(\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{E}[\boldsymbol{\eta}\boldsymbol{\eta}^{T}]\boldsymbol{\Sigma}^{-1}\boldsymbol{A}(\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1} $$
$$ =(\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1}\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{\Sigma}\boldsymbol{\Sigma}^{-1}\boldsymbol{A}(\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1}=(\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1} $$
このように \(\boldsymbol{\gamma}\) は平均 \(\boldsymbol{\hat{\beta}}\) 、分散 \((\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1}\) の \(k\) 次元正規分布であるとわかる。
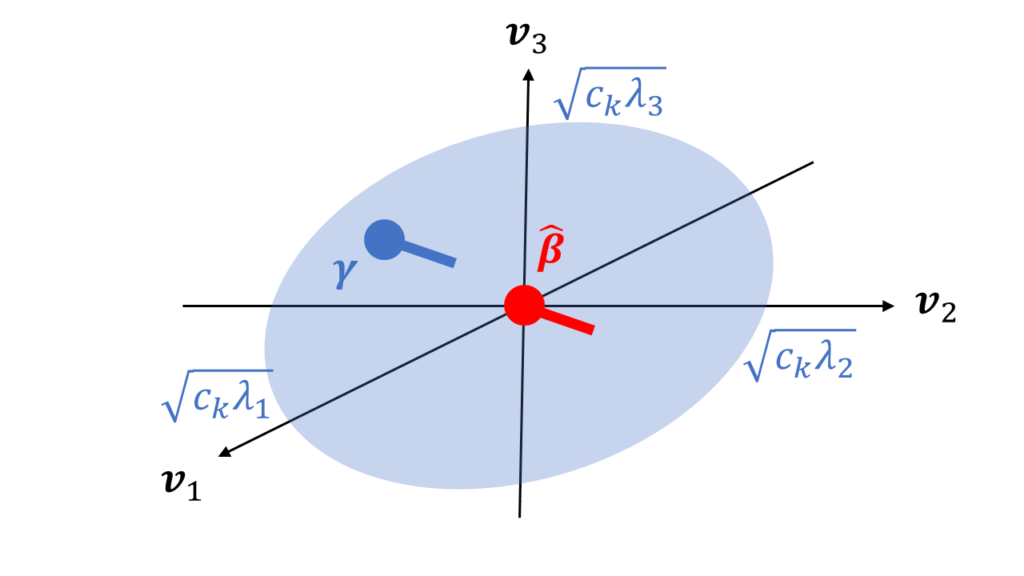
こうして \(\boldsymbol{\gamma}\) について数理統計学的観点から信頼楕円体 confidence ellipsoid を考えることができる。この分散 \((\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1}\) を対称行列なので固有値分解して
$$ (\boldsymbol{A}^{T}\boldsymbol{\Sigma}^{-1}\boldsymbol{A})^{-1}=\boldsymbol{V}\boldsymbol{\Lambda}\boldsymbol{V}^{T} $$
$$ \boldsymbol{\Lambda}=diag\left(\begin{array}{cccc}\lambda_{1} & \lambda_{2} & \ldots & \lambda_{k} \\\end{array}\right) $$
$$ \boldsymbol{V}=\left(\begin{array}{cccc}\boldsymbol{v}_{1} & \boldsymbol{v}_{2} & \ldots &\boldsymbol{v}_{k} \\\end{array}\right) $$
を得る。ただし、\(\lambda_{j}>0\) は固有値、\(\boldsymbol{v}_{j}\) は単位固有ベクトル、\(\boldsymbol{V}\) は直交行列だ
ここで、\(k=5\) 個の独立な標準正規分布の二乗和は \(\chi_{k}^{2}\) 分布だから、\(\chi_{k}^{2}\) 分布の \(p\) パーセンテージ点を \(c_{k}\) とすると、楕円体の式が得られる
$$ \frac{v_{1}^{2}}{\lambda_{1}}+\frac{v_{2}^{2}}{\lambda_{2}}+\ldots+\frac{v_{k}^{2}}{\lambda_{k}}=c_{k} $$
つまり、パラメータ \(\boldsymbol{\gamma}\) によって描かれる信頼楕円体は、次元が \(k=5\)、座標中心が \(\boldsymbol{\hat{\beta}}\)、座標軸が \(\boldsymbol{V}=\left(\begin{array}{cccc}\boldsymbol{v}_{1} & \boldsymbol{v}_{2} & \ldots &\boldsymbol{v}_{k} \\\end{array}\right)\)、軌道半径が
$$ \sqrt{\boldsymbol{\Lambda}}=\sqrt{c_{k}} \ diag\left(\begin{array}{cccc}\sqrt{\lambda_{1}} & \sqrt{\lambda_{2}} & \ldots & \sqrt{\lambda_{k}} \\\end{array}\right) $$
となる。
脳磁図解析において、問題となるのは実際の3次元的な体積だ。すなわち、信頼体積 \(CV\) は \(k=3\) における軌道半径 \(\sqrt{c_{3}\lambda_{1}}, \sqrt{c_{3}\lambda_{2}}, \sqrt{c_{3}\lambda_{3}}\) の楕円体の体積となる。\(\chi_{3}^{2}\) 分布から \(p=0.950\) なら \(c_{3}=7.8147\) であり
$$ CV=\frac{4\pi}{3}\sqrt{c_{3}^{3}\lambda_{1}\lambda_{2}\lambda_{3}}=91.508\sqrt{\lambda_{1}\lambda_{2}\lambda_{3}} $$
を得る
以上から、測定信号を再現するという観点からは GOF が、SNR を考慮して推定電流源の位置を検証するという観点からは CV が提案されていることがわかる。しかしながら、これらには解析の対象とした波形が目的のものとして妥当であるかという根本的な情報は含まれていない。
脳磁図解析の際には数字に惑わされず、波形の視認に立ち返り、波形そのものの妥当性について検討することが最も重要だということがわかる。
まとめ:GOF は単一電流源で測定磁場をどの程度説明できるか、CV は信号が背景ノイズからどの程度突出しているか、についての指標である。これらは各 ECD 推定の妥当性について参考となる指標である。しかしながら、目的となる波形が推定の対象として妥当であるかは、実際に生波形を目視するほかない
次項では、空間フィルターのように議論する電流双極子の数が格子点の数(全脳5mmボクセルならN>10,000)と同じで、センサー数M(=204 or 306)より圧倒的多い状況(劣決定系)での逆問題の解を求めることを考えたい。
References:
- Bagić AI, Knowlton RC, Rose DF, Ebersole JS; ACMEGS Clinical Practice Guideline (CPG) Committee. American Clinical Magnetoencephalography Society Clinical Practice Guideline 1: recording and analysis of spontaneous cerebral activity. J Clin Neurophysiol. 2011 Aug;28(4):348-54.
- Sarvas J. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.
- Hämäläinen M, Hari R, Ilmoniemi R, Knuutila J, Lounasmaa O. Magnetoencephalography theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993 Apr;65(2):413–497.