要旨:脳磁図は脳が発する磁場を測定することで始まる。その主たる起源は大脳皮質にある錐体細胞の樹状突起内におけるシナプス後電位による細胞内電流と考えられている
脳磁図 magnetoencephalography (MEG) における信号の起源(電流)について話を進めていく。
以下の内容は Hämäläinen の総説を読めば事足りるのだが [1]、他の文献も併せて記述する。
脳磁計が測定する磁場の発生源は、大脳皮質第 5 層に分布する錐体細胞 pyramidal cell の樹状突起 dendrite で発生する興奮性シナプス後電位 excitatory postsynaptic potential (EPSP) による細胞内電流 intracellular current だと考えられている。
大脳皮質の主たる神経細胞である錐体細胞は、樹状突起にシナプス結合を受け、興奮性シナプス後電位を生じて細胞内に \(Na^+\), \( Ca^{2+} \) が流入する。
大脳皮質において錐体細胞は皮質表面に対して垂直方向に樹状突起を伸ばしており、細胞膜という絶縁体で覆われているから、樹状突起は皮質表面に対して垂直方向の細胞内電流を生じる(下図)。
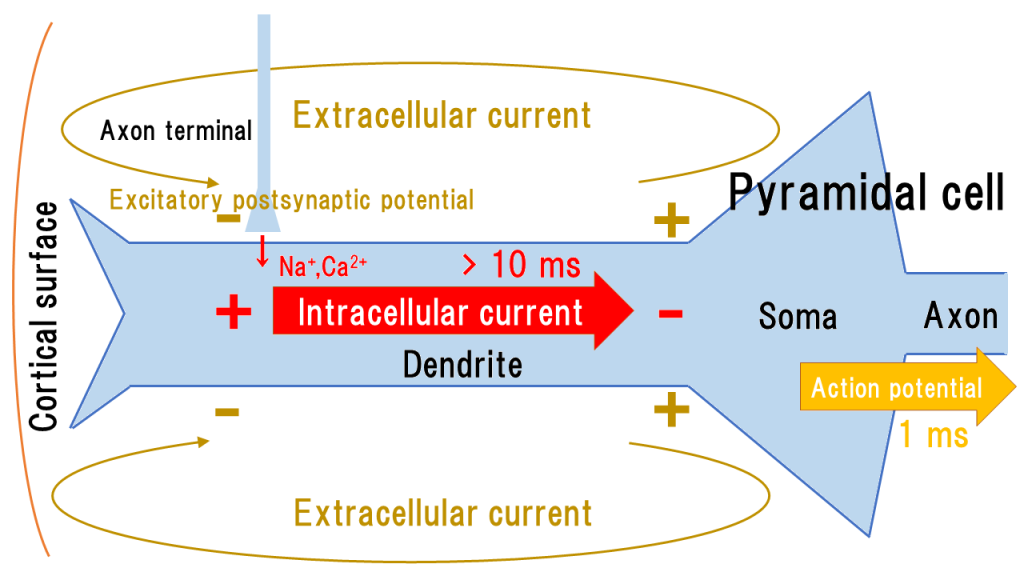
細胞内電流は累積して、軸索を跳躍伝導する活動電位 action potential の原因となる。
細胞内電流はまた、帰還電流である細胞外電流 extracellular current を生じる。
樹状突起の長さは 1 mm 以下であり [2](電流モーメントに寄与するのは 0.1~0.2 mm という説もあり [1])、樹状突起の細胞内電流は点電流に近似できる。後述する理由で磁場に寄与するのは点電流のみとなる。
細胞内電流はシナプス接合部から生じるので、その総体的な向きはシナプスが接続する部位による(例:連合線維・交連線維・視床非特殊核からの線維は大脳皮質表面にある第 1 層に分布するが、視床特殊核からの線維は細胞体 soma 寄りの第 4 層に分布する)。
興奮性シナプス後電位による樹状突起の細胞内電流は数十 ms の幅を持ち、多数の細胞が同期・重畳しやすいため、脳磁計で捉えやすい。
これに対して、軸索を跳躍伝導する活動電位は 1~数 ms 程度の幅しかないので、個々の細胞が同期しづらい。また刺激を強くしても活動電位は重畳するのではなく周波数が上がる(活動の幅が短くなる)ということもわかっている。このように活動電位は脳磁計で捉えづらい(ただし、活動電位は high frequency oscillation との関連が期待されているため、今後の研究課題でもある [1])。
細胞内電流に伴い、細胞外電流も樹状突起周囲に発生する。細胞外電流は細胞外膜という絶縁体の影響を受けないため、細胞外液を広がりながら立体的に流れる(体積電流)。頭皮上脳波で測定される電圧に関与している一方で、脳磁図には関与しない。
一般的な脳磁図の総論・教書では、数式を必要とする順問題の議論(電流はどのようにして磁場を生じるのか、という原因と結果についての議論)を避け、直感的に理解させるために「細胞外電流は対称であり球の外には磁場を形成しない」とか「球対称性により細胞外電流は磁場には寄与しない」とやや曖昧に説明されることが多い [3,4]。
細胞内電流と細胞外電流の磁場への寄与については、次のように Sarvasによる順問題の考察で明らかになる [5]。これにはベクトル解析の知識が必要となる。
全電流密度を \( \boldsymbol{j} \)、源電流密度(細胞内電流)を \( \boldsymbol{j}_i \)、伝導率を \( \sigma \)、電場を \( \boldsymbol{E} \)、電位を \( V \) とすると、体積電流(細胞外電流)は \( \sigma\boldsymbol{E} \) となる。Maxwell 方程式から
$$ \boldsymbol{j}=\boldsymbol{j}_i +\sigma\boldsymbol{E}=\boldsymbol{j}_i -\sigma\boldsymbol{\nabla}V $$
三次元領域 \( G \) について考えると、\( \boldsymbol{j} \) は全電流なので、Biot–Savart の法則が位置 \( \boldsymbol{r} \) における磁場 \( \boldsymbol{b}(\boldsymbol{r}) \) を与える
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’ $$
伝導率 \( \sigma \) が一定の領域において、ラプラシアン \( \Delta \) を用いると
$$ \Delta V=\boldsymbol{\nabla}\cdot\boldsymbol {j}_i / \sigma $$
なので、これを用いて \( \boldsymbol{b}(\boldsymbol{r}) \) を変換していくと
$$ \boldsymbol{b}(\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}dv’ $$
となって磁場 \( \boldsymbol{b}(\boldsymbol{r}) \) は源電流密度 \( \boldsymbol {j}_i \) だけで表現できるので、空間全体が一様な導道率 \( \sigma \) の伝導体において体積電流 \( \sigma\boldsymbol {E} \) は磁場 \( \boldsymbol{b}(\boldsymbol{r}) \) に寄与しない。
この考えを元に、球対称な伝導体を議論していくと、伝導率が不均一であっても磁場の垂直成分 \( b_r (\boldsymbol{r}) \) は
$$ b_r (\boldsymbol{r})=\frac{\mu_0}{4\pi}\int_G \boldsymbol {j}_i(\boldsymbol {r}’)\times\frac{\boldsymbol{r}-\boldsymbol{r}’}{|\boldsymbol{r}-\boldsymbol{r}’|^3}\cdot\boldsymbol {e}_r dv’ $$
となってやはり体積電流 \( \sigma\boldsymbol {E} \) は磁場の垂直成分 \( b_r (\boldsymbol{r}) \) に寄与しない。
この結果を電流双極子で近似し積分することで Sarvas 式 として磁場 \( \boldsymbol{b}(\boldsymbol{r}) \) を得るので、結局のところ体積電流 \( \sigma\boldsymbol {E} \) は磁場 \( \boldsymbol{b}(\boldsymbol{r}) \) に寄与しない。
以上から、脳磁図解析においては点電流に近似できる樹状突起の細胞内電流だけが磁場に寄与すると結論を得る。そしてこの結論は、実験的にも確認されている [6]。
まとめ:錐体細胞は細胞内電流、活動電位、細胞外電流を生じる。このうちで樹状突起における細胞内電流が脳磁計の検出する磁場を生じているのだと考えられている
次項 では、点電流についてもう少し考察し、脳磁図における電流を議論する土台となる電流双極子の概念を導入する。
(引用)
- MS Hämäläinen, R Hari, RJ Ilmoniemi, J Knuutila, OV Lounasmaa: Magnetoencephalography theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993 Apr;65(2):413-97.
- Benavides-Piccione R, Hamzei-Sichani F, Ballesteros-Yáñez I, DeFelipe J, Yuste R. Dendritic size of pyramidal neurons differs among mouse cortical. Cereb Cortex. 2006 Jul;16(7):990-1001.
- Hansen Peter, Morten Kringelbach, and Riitta Salmelin (eds), MEG: An Introduction to Methods. New York, 2010; online edn, Oxford Academic, 1 Sept. 2010.
- Hari Riitta and Puce Aina (eds), MEG-EEG Primer. New York, 2017; online edn, Oxford Academic, 1 Mar. 2017.
- J Sarvas. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys Med Biol. 1987 Jan;32(1):11-22.
- Okada YC, Nicholson C. Magnetic evoked field associated with transcortical currents in turtle cerebellum. Biophys J. 1988 May;53(5):723-31.